热传递的经典动力学理论
气体动力学理论
在经典气体动力学理论中,设一个分子在传播过程中移动的总路径为 $L$。该分子在此过程中“扫过”的有效体积为 $\pi d^2 L$,其中 $d$ 为分子的直径。若气体的分子数密度为 $n$,则该体积内平均含有 $\pi n d^2 L$ 个分子,因此该分子在此路径上经历的碰撞次数为:
\[N = \pi n d^2 L\]定义两次碰撞之间的平均自由程为 $\Lambda$,即:
\[\Lambda = \frac{L}{N} = \frac{L}{\pi n d^2 L} = \frac{1}{n \sigma}\]其中,$\sigma = \pi d^2$ 被称为分子的碰撞截面。
将理想气体状态方程中的密度表达式 $n = \frac{p}{k_B T}$ 代入上式,得到平均自由程的形式为:
\[\Lambda = \frac{k_B T}{p \sigma}\]为了计算理想气体的热流密度,我们从单个分子的角度考虑。设其内能为 $\varepsilon$,沿 $x$ 方向的速度分量为 $v_x$,则单位时间内该分子沿 $x$ 方向传递的能量近似为:
\[q_x = \frac{1}{2} v_x \left[\varepsilon(x - \Lambda_x) - \varepsilon(x + \Lambda_x)\right]\]展开为泰勒级数并忽略高阶项,有:
\[q_x \approx -v_x \Lambda_x \frac{\mathrm{d} \varepsilon}{\mathrm{d}x} \approx -(\cos^2\theta) v \Lambda \frac{\mathrm{d} \varepsilon}{\mathrm{d}x}\]对所有角度进行积分(假设各向同性)可得总热流为:
\[q_x = -\frac{1}{2\pi} v \Lambda \frac{\mathrm{d} \varepsilon}{\mathrm{d}x} \left[\int_0^{2\pi} \mathrm{d}\varphi \int_0^{\pi/2} \cos^2\theta \sin\theta \, \mathrm{d}\theta \right] \frac{\mathrm{d} \varepsilon}{\mathrm{d}T} \frac{\mathrm{d}T}{\mathrm{d}x}\]最终简化为:
\[q_x \approx -\frac{1}{3} C v \Lambda \frac{\mathrm{d}T}{\mathrm{d}x}\]由此推得热导率表达式:
\[\lambda = \frac{1}{3} C v \Lambda\]这表明气体的热导率与比热容 $C$、分子热速 $v$ 和平均自由程 $\Lambda$ 成正比。
电介质中的传热
在绝缘体或半导体等电介质中,热量的传递主要由晶格振动激发出的准粒子——声子承担。每个声子的能量为 $\hbar \omega$,其中 $\omega$ 为振动频率。
声子的热导率也可用类似的公式表达为:
\(\lambda_{ph} = \frac{1}{3} C_{ph} v_s \Lambda_{\Sigma}\) 其中:
- $C_{ph}$ 是声子系统的比热容;
- $v_s$ 是有效声速;
- $\Lambda_{\Sigma}$ 是综合平均自由程。
声子的散射机制主要包括:
- 声子-边界散射($b$);
- 声子-杂质散射($imp$);
- 声子-声子散射($ph$)。
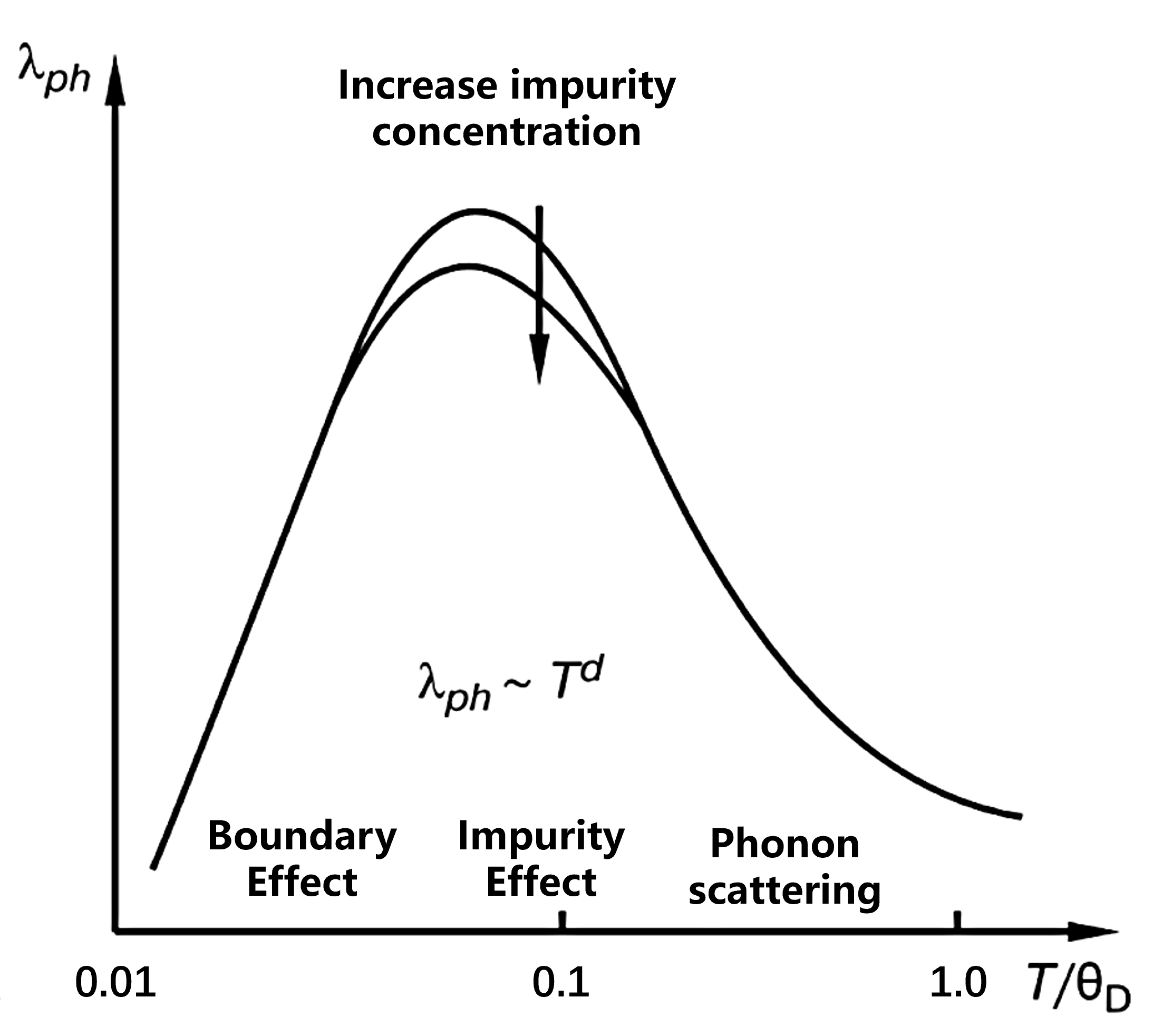
根据 Matthiessen 规则,这些散射机制的贡献是可加的,其倒自由程满足:
\[\Lambda_{\Sigma}^{-1} = \Lambda_{ph}^{-1} + \Lambda_{imp}^{-1} + \Lambda_{b}^{-1}\]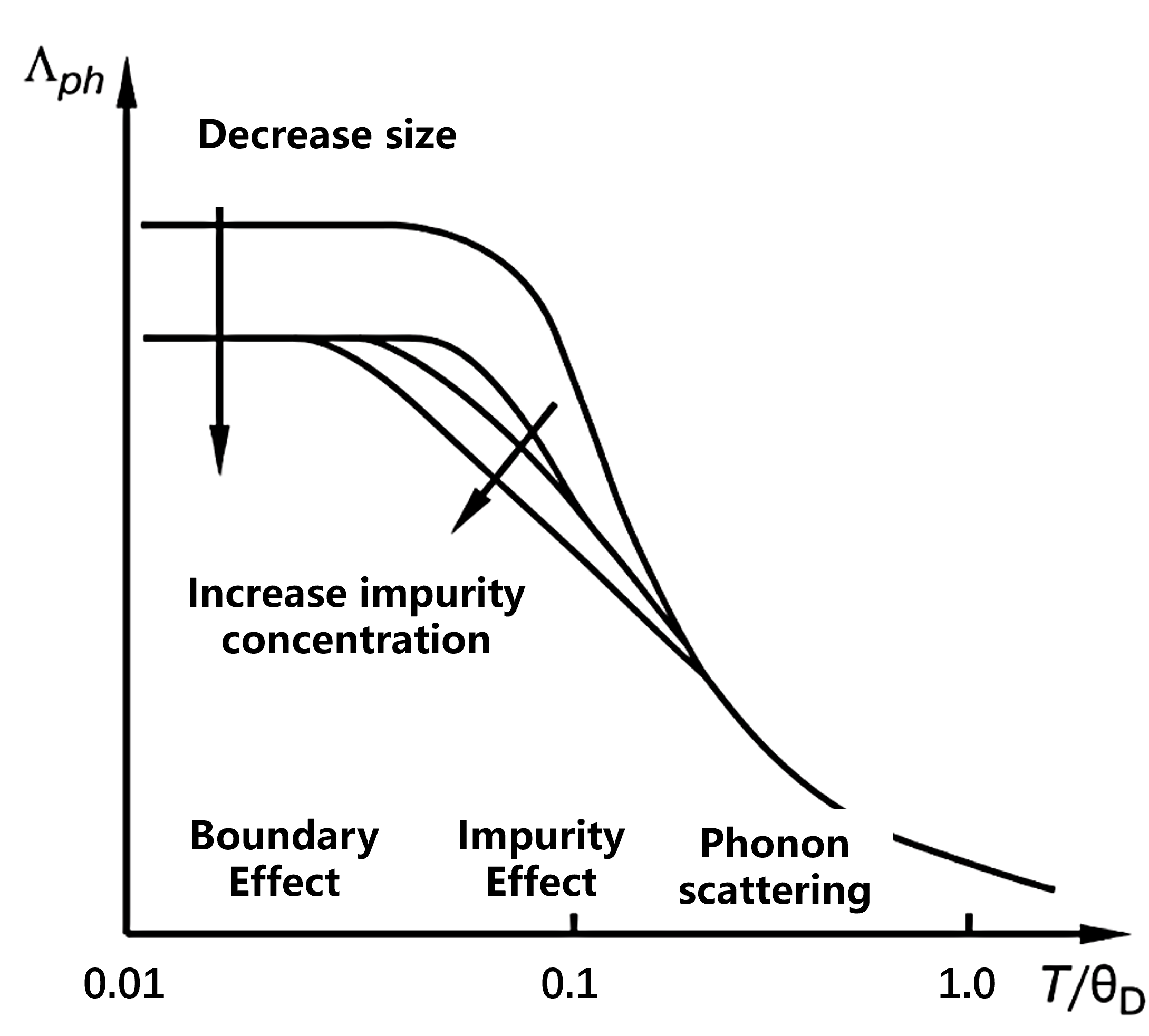
金属中的传热
在金属中,热量的主要载流子是自由电子。电子气体的热导率可以由下式表示:
\[\lambda_{e} = \frac{1}{3} C_{e} v_F \Lambda_{e}\]其中:
- $C_e$ 为电子系统的比热;
- $v_F$ 为费米速度;
- $\Lambda_e$ 为电子的平均自由程。
电子的散射机制也可按 Matthiessen 规则处理:
\[\frac{1}{\Lambda_e} = \frac{1}{\Lambda_{ph}} + \frac{1}{\Lambda_d} + \frac{1}{\Lambda_b}\]玻尔兹曼输运方程
在微观尺度上,传热过程由粒子的分布函数描述。若系统处于平衡,则粒子分布函数为平衡分布 $f(\varepsilon, T)$,其形式根据粒子统计不同可为:
- 麦克斯韦-玻尔兹曼分布(经典气体);
- 玻色-爱因斯坦分布(如声子);
- 费米-狄拉克分布(如电子)。
当系统远离平衡态时,分布函数变为非平衡形式 $f(\vec{r}, \vec{p}, t)$,其演化由 玻尔兹曼输运方程 控制:
\[\frac{\partial f}{\partial t} + \vec v \cdot \nabla_{\vec r} f + \vec F \cdot \nabla_{\vec p} f = \left(\frac{\partial f}{\partial t}\right)_\text{st}\]其中,右边的碰撞项 $\left(\partial f / \partial t\right)_{\text{st}}$ 描述系统通过各种相互作用趋向平衡的过程。
傅里叶定律与传热方程
在宏观尺度上,热传导满足经典的 傅里叶定律:
\[\vec q = -\lambda \nabla T\]将其代入能量守恒的传热方程:
\[\rho C_p \frac{\partial T}{\partial t} = -\nabla \cdot \vec q\]得到 热扩散方程:
\[\rho C_p \frac{\partial T}{\partial t} = \lambda \nabla^2 T \quad \Rightarrow \quad \frac{\partial T}{\partial t} = a \nabla^2 T\]其中 $a = \frac{\lambda}{\rho C_p}$ 是热扩散系数,描述温度扰动在介质中的扩散速率。
总结
- 传热性质不仅取决于材料的本征参数(如比热、速度、自由程),还受结构尺寸和时间尺度的影响。
- 当系统特征尺寸小于平均自由程时,傅里叶定律不再适用,应使用玻尔兹曼输运方程或分子动力学方法建模。
- 若系统尺寸接近载流子波长,波动效应变得显著,需要引入波动传播模型(如声子干涉或局域化理论)进行分析。