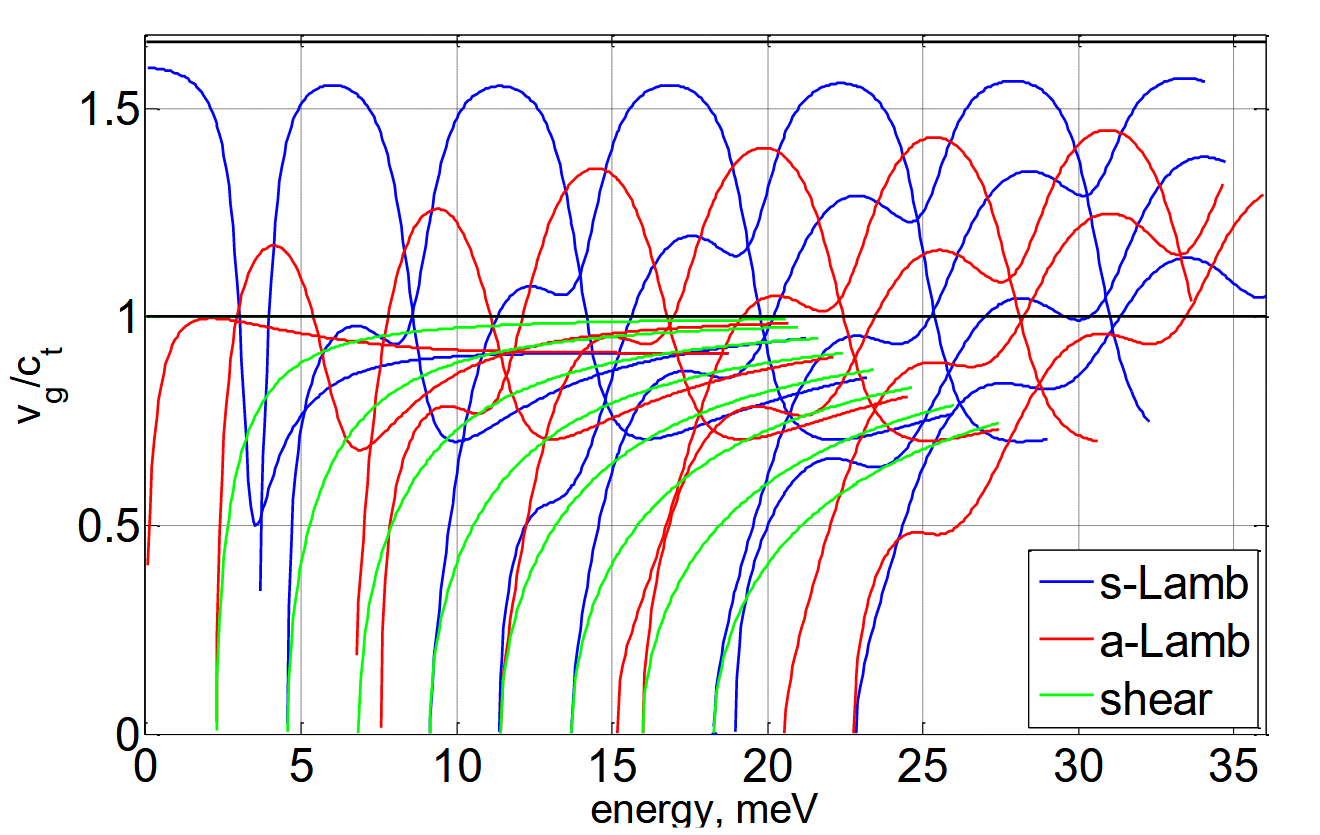
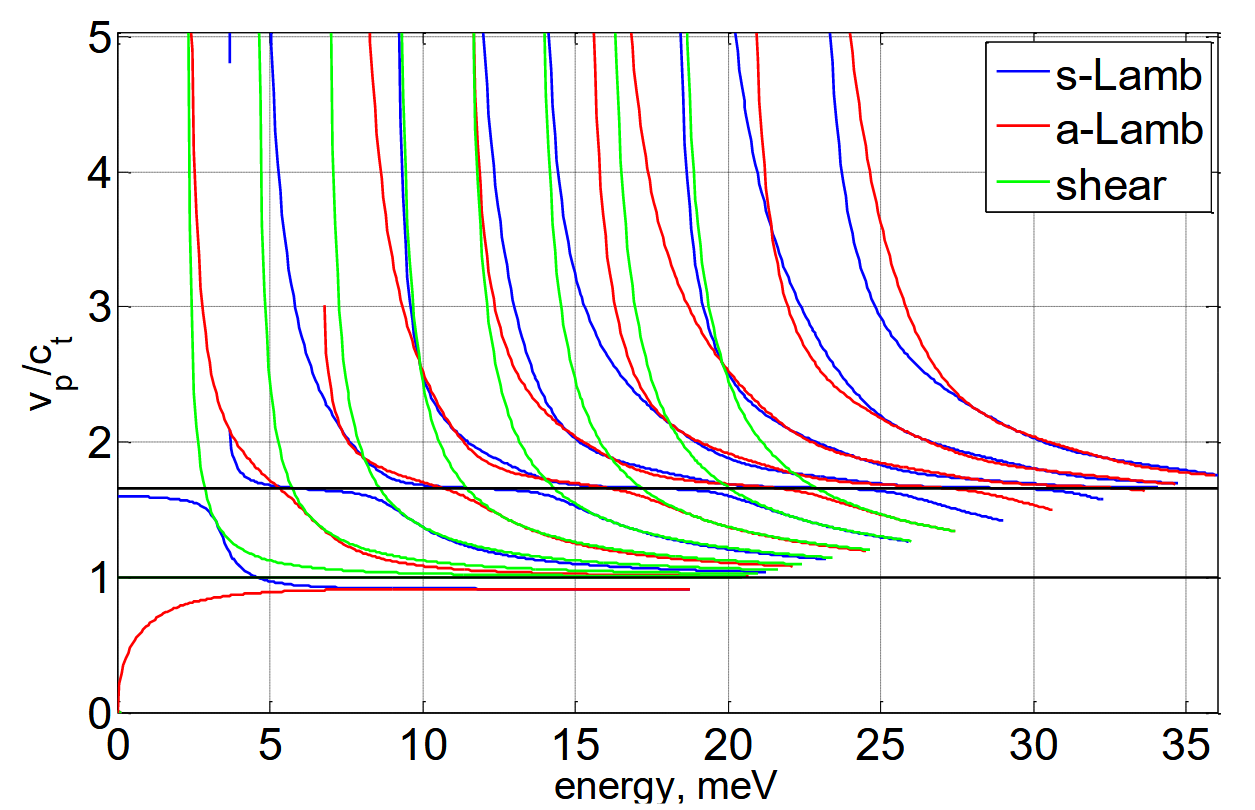
平板中的弹性波色散关系
本文基于求解连续介质的弹性方程来研究波动过程。
在平板中,波可以分为 纵波(P波)与 横波(S波),S 波又分为 SH 波 和 SV 波。
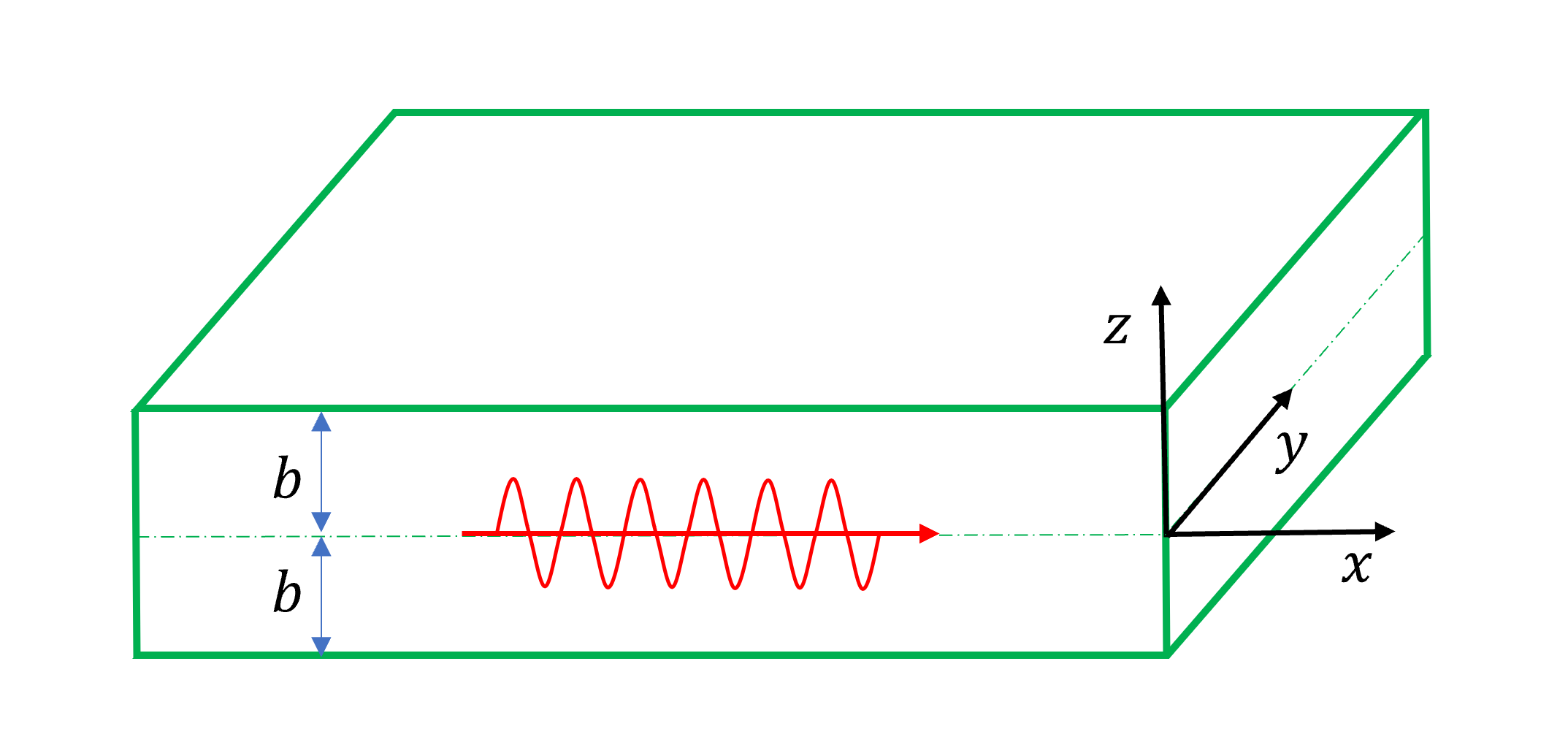
假设波的传播方向为 $x$ 轴。质点振动发生在 $x$ 轴方向的为 P 波,质点振动发生在 $y$ 轴方向的为 SH 波,质点振动发生在 $z$ 轴方向的为 SV 波。
SV 波和 P 波在平板表面无应力的条件下耦合为 Rayleigh-Lamb 波。
弹性波动方程
在连续介质近似中,考虑在平板中沿 $x$ 方向传播的弹性波,波动方程为:
\[\mu\Delta\vec u+(\lambda+\mu)\nabla(\nabla\vec u) = \rho \frac{\partial^2 \vec u}{\partial t^2}\]其中 $\vec u$ 是位移矢量; $\lambda + \mu$ 是 Lame 常数,取决于介质的弹性特性;$\rho$ 为介质密度。
波动方程的所有解都可以表示为标量势 $\varphi$ 和向量势 $\vec\psi$ 的组合:
\[\vec u =\text{grad }\varphi + \text{rot }\vec\psi\]SH 波的色散关系
SH 波中原子的位移发生在 $y$ 轴方向,即位移矢量为 $\vec u = (0,u_y,0)$。
因此,SH 波的波动方程为:
\[\frac{\partial^2 u_y}{\partial x^2}+\frac{\partial^2 u_y}{\partial z^2} = \frac{1}{c_t^2}\frac{\partial^2 u_y}{\partial t^2}\]其中 $c_t=\sqrt{\mu/\rho}$ 为剪切波的速度。
解为:
\[u_y=(A_1\sin\beta z + A_2\cos\beta z)e^{i(\xi x-\omega t)}\]其中 $\xi$ 为波矢在 $x$ 轴上的投影; $\omega$ 为频率;$\beta$ 是波矢在 $z$ 轴上的投影,满足关系式:
\[\beta^2+\xi^2=\frac{\omega^2}{c_t^2}\]我们考虑平板表面无应力,所以边界条件为:
\[\tau_{zy} =\mu\frac{\partial u_y}{\partial z}=0,~~y=\pm b\]将波动方程的解代入边界条件中,得到
\[A_1\cos\beta b-A_2\sin\beta b =0 \\ A_1\cos\beta b+A_2\sin\beta b =0\]由此,得到频率方程:
\[\cos\beta b\sin \beta b=0\]该方程满足:
\[\beta b = n\pi/2~~~(n=0,1,2,3,...)\]最终得出 SH 波的色散关系:
\[\omega^2=c_t^2\left[\xi^2+\left(n\pi/2b\right)^2\right]\]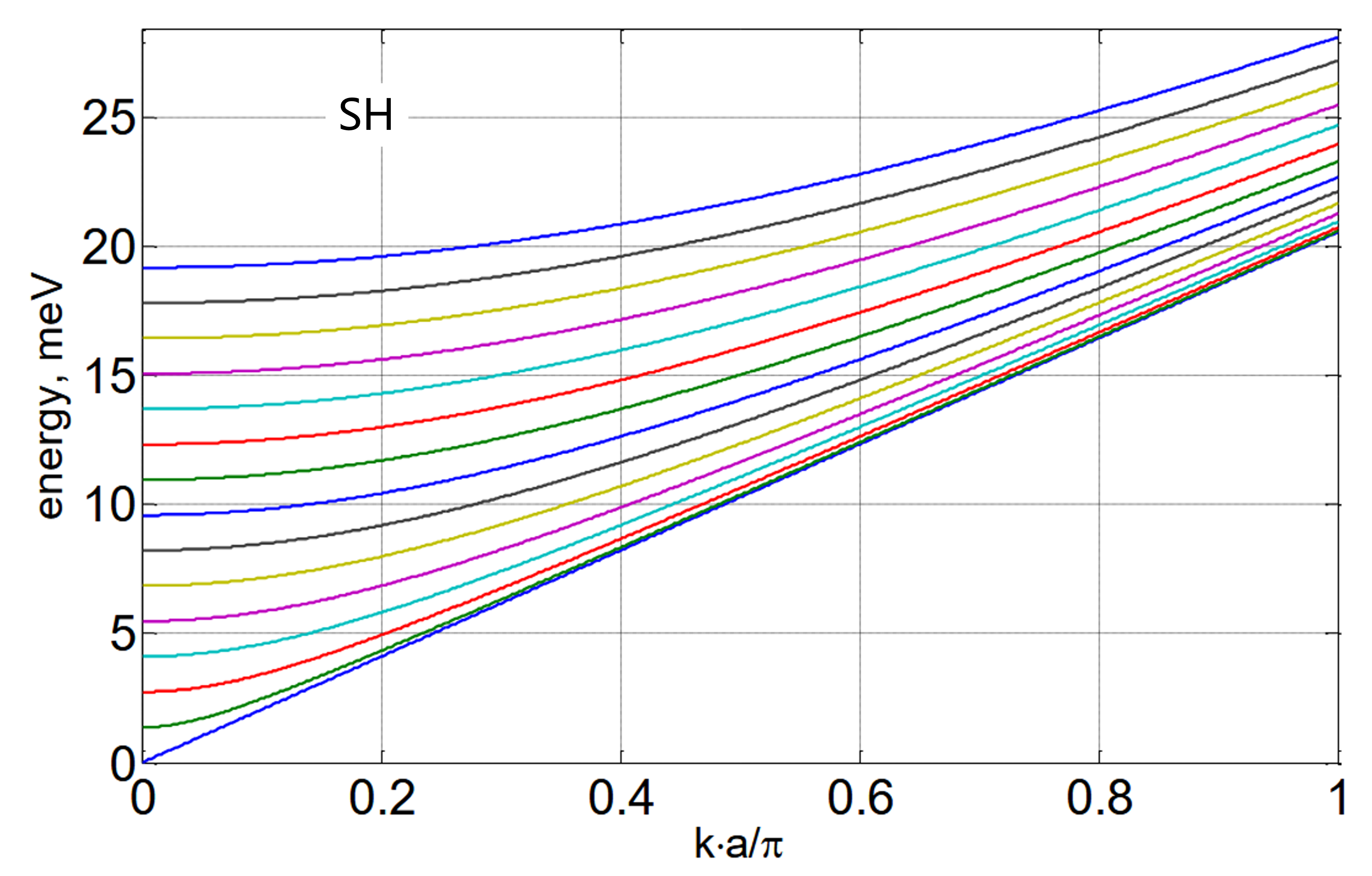
Rayleigh-Lamb 波的色散关系
考虑在具有无应力边界的厚度为 2b 的板中同时存在 P 波和 SV 波。
由于原子运动不依赖于 $y$ 坐标,位移矢量为 $\vec u = (u_x,0,u_z)$,标量势为 $\psi$,向量势为 $\vec\psi=(0,\psi_y,0)$。
Rayleigh-Lamb 波的波动方程为:
\[\frac{\partial^2 \varphi}{\partial x^2}+\frac{\partial^2 \varphi}{\partial y^2}=\frac{1}{c_l^2}\frac{\partial \varphi}{\partial t^2}\] \[\frac{\partial^2 \psi_y}{\partial x^2}+\frac{\partial^2 \psi_y}{\partial y^2}=\frac{1}{c_t^2}\frac{\partial \psi_y}{\partial t^2}\]其中 $c_l=\sqrt{(\lambda+2\mu)/\rho}$ 是膨胀波的速度;$c_t=\sqrt{\mu/\rho}$ 为剪切波的速度。
考虑波动方程的解为:
\[\varphi=(A\sin\alpha z+B\cos\alpha z)e^{i(\xi x-\omega t)}\] \[\psi_y=i(C\sin\beta z+ D\cos\beta z)e^{i(\xi x-\omega t)}\] \[u_x=i\{\xi(A\sin\alpha z+B\cos\alpha z)+\beta(C\cos\beta z-D\sin\beta z)\}e^{i(\xi x-\omega t)}\] \[u_z=\{\alpha(A\cos\alpha z-B\sin\alpha z)+k(C\sin\beta z+ D\cos\beta z)\}e^{i(\xi x-\omega t)}\]边界条件为:
\[\tau_{zz} = \tau_{xz} =0,~~~z=\pm b\]现在,我们将分别考虑对称波和非对称波的情况。
对称波
应用 $A=D=0$,位移为:
\[u_x=i(Bk\cos\alpha z+ C\beta\cos\beta z)e^{i(\xi x-\omega t)}\] \[u_z=(-B\alpha\sin\alpha z)+Ck\sin\beta z)e^{i(\xi x-\omega t)}\]此时 $\tau_{zz}$ 和 $\tau_{xz}$ 的边界条件为:
\[(\xi^2-\beta^2)B\cos\alpha b+2\xi\beta C\cos\beta b=0 \\ \pm i\left[-2\alpha \xi B\sin\alpha b+(\xi^2-\beta^2)C\sin\beta b\right]=0\]得到对称波在平板中传播的 Rayleigh-Lamb 频率方程:
\[\frac{\tan\beta b}{\tan\alpha b} = -\frac{4\alpha\beta \xi^2}{(\xi^2-\beta^2)^2}\]反对称波
应用 $B=C=0$,位移为:
\[u_x = i \bigg(\xi A\sin\alpha z - \beta D\sin\beta z\bigg) e^{i(\xi x-\omega t)}\] \[u_z = \bigg(\alpha A\cos\alpha z + \xi D\cos\beta z\bigg) e^{i(\xi x-\omega t)}\]此时 $\tau_{zz}$ 和 $\tau_{xz}$ 的边界条件简化为:
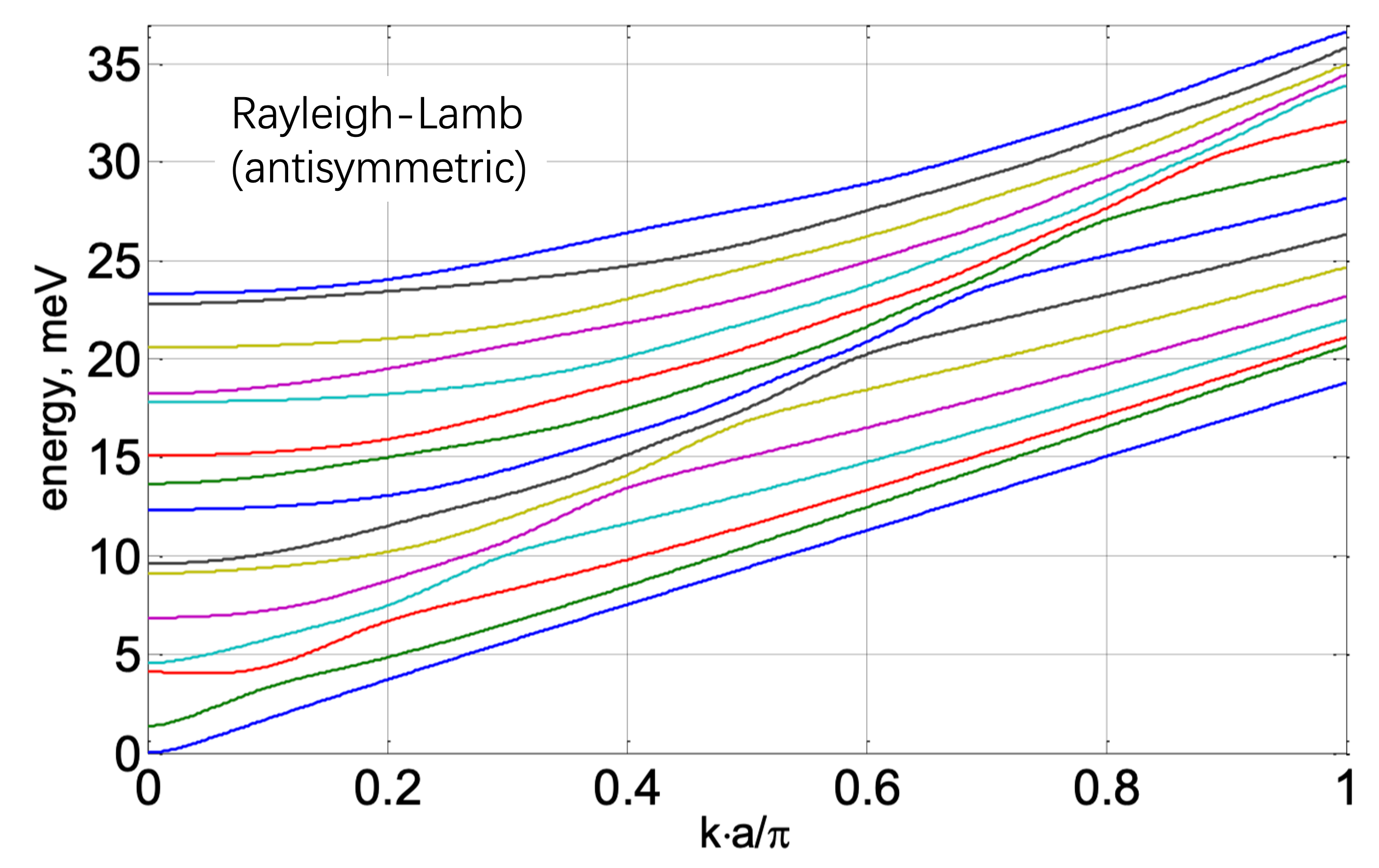
\[\pm \bigg[ \bigg(\xi^2-\beta^2\bigg)A\sin\alpha b - 2\beta \xi D \sin\beta b \bigg] = 0\] \[2\alpha \xi A\cos\alpha b - \bigg(\beta^2-\xi^2\bigg) D\cos\beta b = 0\]得到反对称波在平板中传播的 Rayleigh-Lamb 频率方程:
\[\frac{\tan\beta b}{\tan\alpha b} = -\frac{\bigg(\xi^2-\beta^2\bigg)^2}{4\alpha\beta \xi^2}\]3.3 Rayleigh-Lamb 频率方程
将对称波和非对称波的频率方程组合成一个方程,如下所示:
\[F(\alpha,\beta,\xi) = \frac{\tan\beta b}{\tan\alpha b} + \bigg(\frac{4\alpha\beta \xi^2}{\big(\xi^2-\beta^2\big)^2}\bigg)^{\pm 1} = 0\]我们知道:
\[\alpha^2 = \frac{\omega^2}{c_l^2} - \xi^2 = \xi^2 \bigg(\frac{c^2}{c_l^2} - 1\bigg)\] \[\beta^2 = \frac{\omega^2}{c_t^2} - \xi^2 = \xi^2 \bigg(\frac{c^2}{c_t^2} - 1\bigg)\]可以看出,$\alpha$、$\beta$ 可能为实数、零或虚数。然后频率方程也相应地改变:
区域 I: \(\xi > \frac{\omega}{c_t}\) (也可以表示为:\(c < c_l, c_t\))
我们用 $i\alpha’$, $i\beta’$ 代替频率方程中的 $\alpha$, $\beta$ (其中,$\alpha’^2 = -\alpha^2, ~\beta’^2 = -\beta^2$),得到:
\[\frac{\tan\beta' b}{\tan\alpha' b} = -\bigg(\frac{4\alpha'\beta' \xi^2}{\big(\xi^2-\beta'^2\big)^2}\bigg)^{\pm 1}\]区域 II: $\frac{\omega}{c_t} > \xi > \frac{\omega}{c_l}$ (也可以表示为:$c_t < c < c_l$)
我们用 $i\alpha’$ 代替频率方程中的 $\alpha$(其中,$\alpha’^2 = -\alpha^2$),得到:
\[\frac{\tan\beta b}{\tan\alpha' b} = -\bigg(\frac{4\alpha'\beta \xi^2}{\big(\xi^2-\beta^2\big)^2}\bigg)^{\pm 1}\]区域 III: $\xi < \frac{\omega}{c_l}$ (也可以表示为:$c > c_l$)
频率方程和之前一致:
\[\frac{\tan\beta b}{\tan\alpha b} = -\bigg(\frac{4\alpha\beta \xi^2}{\big(\xi^2-\beta^2\big)^2}\bigg)^{\pm 1}\]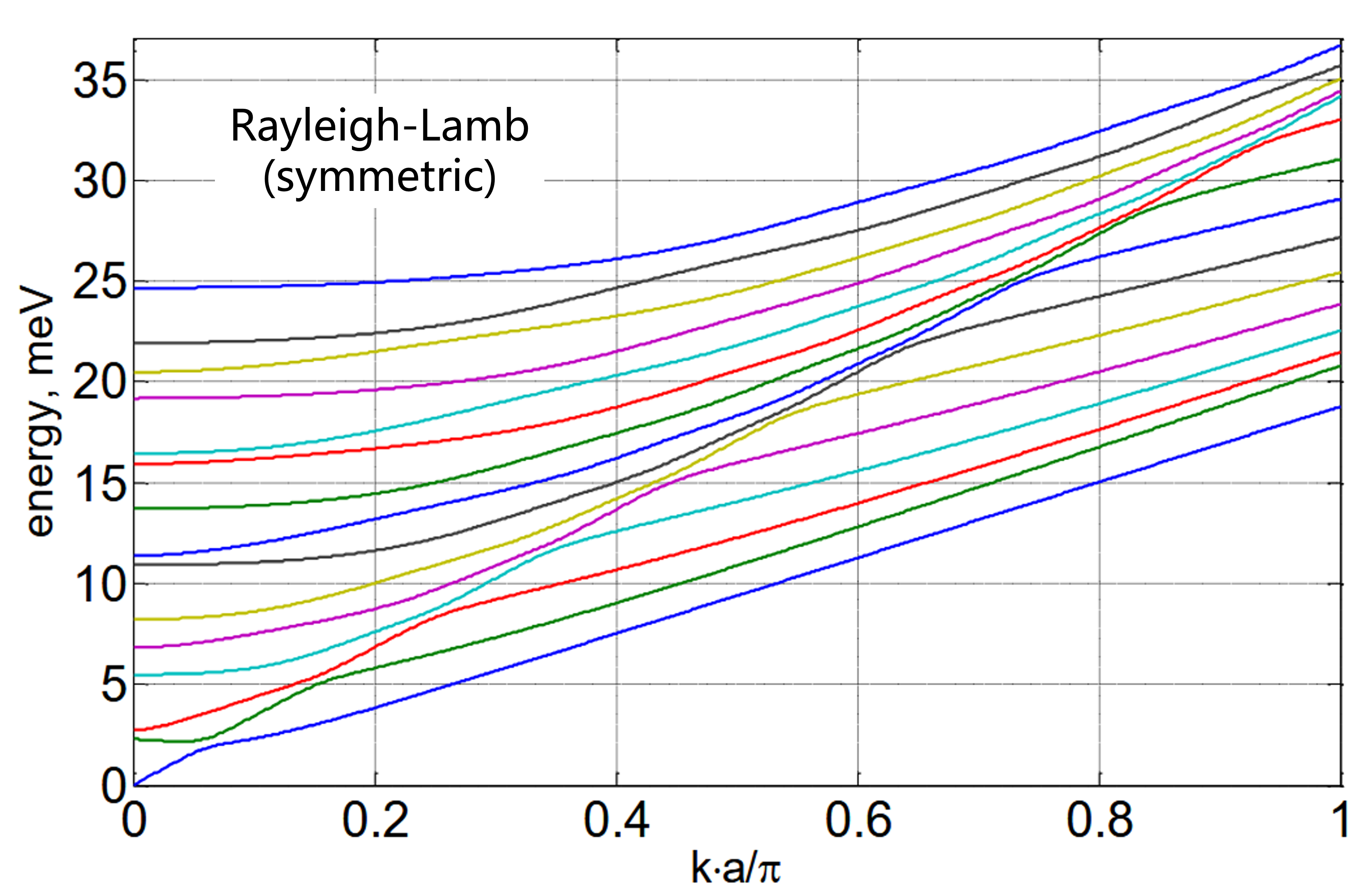
群速度与相速度
相速度是波相在给定方向上的传播速度:
\[v_p=\frac{\omega}{k}\]群速度是介质中能量传递的速度:
\[v_g=\frac{\partial\omega}{\partial k}\]