圆棒中的弹性波色散关系
圆棒中的弹性方程
弹性波动的一般方程:
\[\mu \nabla^2\vec u=(\lambda+\mu)\nabla(\nabla\cdot\vec u)=\rho\frac{\partial^2\vec u}{\partial t^2}\]其中 $\vec u$ 是位移矢量; $\lambda$ , $\mu$ – 表征介质弹性特性的 Lame 常数; $\rho$ 是密度,$t$ 是时间。
将位移矢量 $\vec u$ 表示为标量势 $\varphi$ 和矢量势 $\vec\psi$ 的组合。
\[\vec u=\nabla\varphi+\nabla\times\vec\psi\]将位移向量代入弹性波动方程,可得:
\[\nabla^2\varphi=\frac{1}{c_l^2}\frac{\partial^2\varphi}{\partial t^2},~ \nabla^2\vec\psi=\frac{1}{c_t^2}\frac{\partial^2\vec\psi}{\partial t^2}\]其中 $c_l=\sqrt{(\lambda+2\mu)/\rho}$ 是膨胀波的速度,$c_t=\sqrt{\mu/\rho}$ 是剪切波的速度。
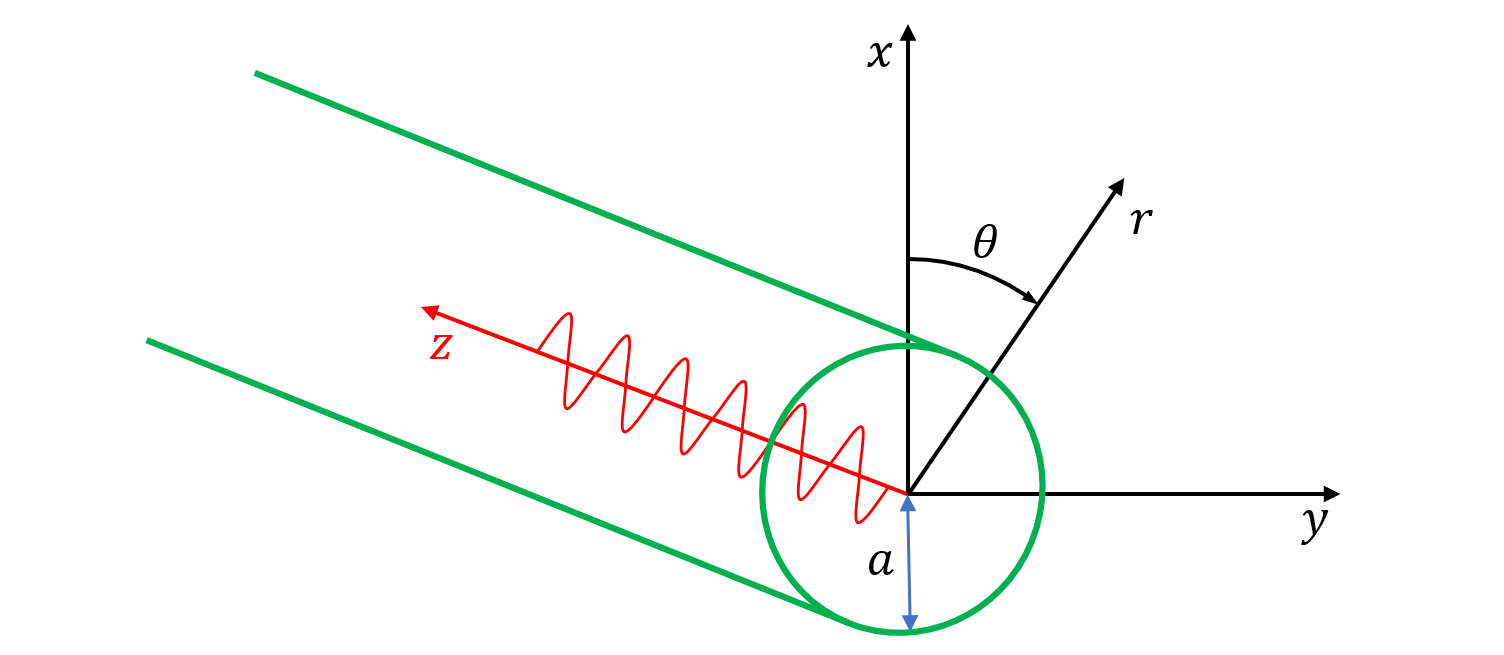
在柱坐标系中,位移分量为:
\[u_r=\frac{\partial\varphi}{\partial r}+\frac{1}{r}\frac{\partial\psi_z}{\partial\theta}-\frac{\partial\psi_\theta}{\partial z}\] \[u_\theta=\frac{1}{r}\frac{\partial\varphi}{\partial\theta}+\frac{\partial\psi_r}{\partial z}-\frac{\partial\psi_z}{\partial r}\] \[u_z=\frac{\partial\varphi}{\partial z}+\frac{1}{r}\frac{\partial(\psi_\theta r)}{\partial r}-\frac{1}{r}\frac{\partial\psi_r}{\partial\theta}\]应力为:
\[\tau_{rr}=\lambda\left(\frac{\partial u_r}{\partial r}+\frac{u_r}{r}+\frac{1}{r}\frac{\partial u_\theta}{\partial\theta}+\frac{\partial u_z}{\partial z}\right)+2\mu\frac{\partial u_r}{\partial r}\] \[\tau_{r\theta}=\mu\left(\frac{\partial u_\theta}{\partial r}-\frac{u_\theta}{r}+\frac{1}{r}\frac{\partial u_r}{\partial\theta}\right)\] \[\tau_{rz}=\mu\left(\frac{\partial u_r}{\partial z}+\frac{\partial u_z}{\partial r}\right)\]考虑半径为 $a$ 的实心无限长圆棒。 假设圆棒表面无应力,即边界条件如下:
\[\tau_{rr}=\tau_{r\theta}=\tau_{rz}=0,~~~r=a\]扭转波

扭转波仅存在周向位移分量 $u_\theta$ :
\[u_\theta=\frac{1}{\beta}BJ_1(\beta r)\exp[i(\xi z-\omega t)]\]根据边界条件,得到扭转波的频率方程:
\[\beta a\cdot J_0(\beta a)-2J_1(\beta a)=0\]色散关系:
\[\omega^2=c_t^2(\xi^2+\beta^2)\]通过引入 $\overline\alpha=\alpha a$ $\overline\alpha=\alpha a$$\overline\beta=\beta a$,$\overline\xi=\xi a$ 和 $\Omega=\omega a/c_t$,得到无量纲色散关系:
\[\Omega^2=\overline\xi^2+\overline\beta^2\]纵波
纵波是轴对称波,存在径向位移分量 $u_r$ 和轴向位移分量 $u_z$ :
\[u_r=[-\alpha AJ_1(\alpha r)-ikCJ_1(\beta r)]\exp[i(\xi z-\omega t)]\] \[u_z=[ikAJ_0(\alpha r)+\beta CJ_0(\beta r)]\exp[i(\xi z-\omega t)]\]根据边界条件,得到纵波的频率方程:
\[(\xi^2-\beta^2)^2\frac{(\alpha a)J_0(\alpha a)}{J_1(\alpha a)}+4k^2\alpha ^2\frac{(\beta a)J_0(\beta a)}{J_1(\beta a)}=2\alpha ^2(\xi^2+\beta ^2)\]色散关系:
\[\omega^2=c_t^2(\xi^2+\beta^2)=c_l^2(\xi^2+\alpha^2)\]通过引入 $\overline\alpha=\alpha a$ $\overline\alpha=\alpha a$$\overline\beta=\beta a$,$\overline\xi=\xi a$ 和 $\Omega=\omega a/c_t$,得到无量纲色散关系:
\[\Omega^2=\overline\xi^2+\overline\beta^2 = (c_l/c_t)^2(\overline\xi^2+\overline\alpha^2)\]弯曲波
对于弯曲波,必须考虑所有三个位移分量:
\[u_r=\left[A\frac{\partial}{\partial r}J_1(\alpha r)+\frac{B}{r}J_1(\beta r)+ikCJ_2(\beta r)\right]\cos(\theta)\exp[i(\xi z-\omega t)]\] \[u_\theta=\left[-\frac{A}{r}J_1(\alpha r)+ikCJ_2(\beta r)-B\frac{\partial}{\partial r}J_1(\beta r)\right]\cos(\theta)\exp[i(\xi z-\omega t)]\] \[u_z=\left[ikAJ_1(\alpha r)-\frac{C}{r}\frac{\partial}{\partial r}[rJ_2(\beta r)]-\frac{C}{r}J_2(\beta r)\right]\cos(\theta)\exp[i(\xi z-\omega t)]\]根据边界条件,得到弯曲波的频率方程:
\[J_1(\overline\alpha)J_1^2(\overline\beta) \begin{vmatrix} \overline\xi^2-\overline\beta^2+4-2\Psi_\alpha & 2\overline\xi(\overline\beta^2-2+\Psi_\beta) & 2\Psi_\beta-4 \\ 4-2\Psi_\alpha & 2\overline\xi(\Psi_\beta-2) & \overline\beta^2-4+2\Psi_\beta \\ 2\overline\xi(\Psi_\alpha-1) & (\overline\beta^2-\overline\xi^2)(\Psi_\beta-1) & \overline\xi \end{vmatrix} =0\] \[\Psi_\alpha = \overline\alpha J_0(\overline\alpha)/J_1(\overline\alpha)\] \[\Psi_\beta = \overline\beta J_0(\overline\beta)/J_1(\overline\beta)\]无量纲色散关系:
\[\Omega^2=\overline\xi^2+\overline\beta^2 = (c_l/c_t)^2(\overline\xi^2+\overline\alpha^2)\]数值求解
根据 $\alpha$ 是实数还是虚数,可以分为两个区域:
区域 I:$\omega>c_l\xi$, $\alpha$ 是实数
区域 II:$\omega<c_l\xi$, $\alpha$ 是虚数,用 $i\alpha’$代替 $\alpha$(其中,$\alpha’^2=-\alpha^2$)。
针对不同的区域,采用下列寻根方法:
第一步,在波矢值最小处通过遍历确定两组根。
第二步,根据前两组根逐层自适应对方程进行求解。