热物理学的微观描述

传热学中的宏观能量守恒方程描述热能的储存、传输（热传导 $k$、热对流 $u$ 和热辐射 $r$）以及与其他形式的能量之间的转换。

能量守恒方程

\[\nabla\cdot \boldsymbol q=-\rho c_p\frac{\partial T}{\partial t}+\sum_{i,j}\dot s_{i-j}, \nabla\cdot \boldsymbol q=\frac{\int_{\Delta A}(\boldsymbol q\cdot\boldsymbol s_{\boldsymbol n})dA}{\Delta V \to 0}\]

其中，$\rho c_p\frac{\partial T}{\partial t}$ 被称为显热储存，$\dot s_{i-j}$ 为热能的能量转换速率，由能量载流子 $i$ 和 $j$ 之间相互作用的性质和频率决定。

热流矢量 $\boldsymbol q$ 是传导、对流和辐射热流矢量之和：

\[\boldsymbol q = \boldsymbol q_k + \boldsymbol q_u + \boldsymbol q_r\]

传导热流矢量 $\boldsymbol q_k$ 是热导率 $k$ 与温度梯度 $\nabla T$ 乘积的负数，即傅立叶传导定律：

\[\boldsymbol q_k = -k\nabla T\]

对流热流矢量 $\boldsymbol q_u$ 是 $\rho c_p$、局部速度矢量 $\boldsymbol u$ 和温度 $T$ 的乘积：

\[\boldsymbol q_u = \rho c_p\boldsymbol u T\]

辐射热流矢量 $\boldsymbol q_r$ 是对单位矢量 $\boldsymbol s$ 与电磁谱的定向辐射强度 $I_{ph,\omega}$ 乘积在空间上和电磁谱上的积分：

\[\boldsymbol q_r = 2\pi\int_0^\infty\int_{-1}^1\boldsymbol s I_{ph,\omega}d\mu d\omega\]

主要的能量载流子

四种能量载流子，即：声子 ($p$)、电子 ($e$)、流体粒子 ($f$) 和光子 ($ph$)，构建了热能存储、传输和相互作用的微观模型。

声子

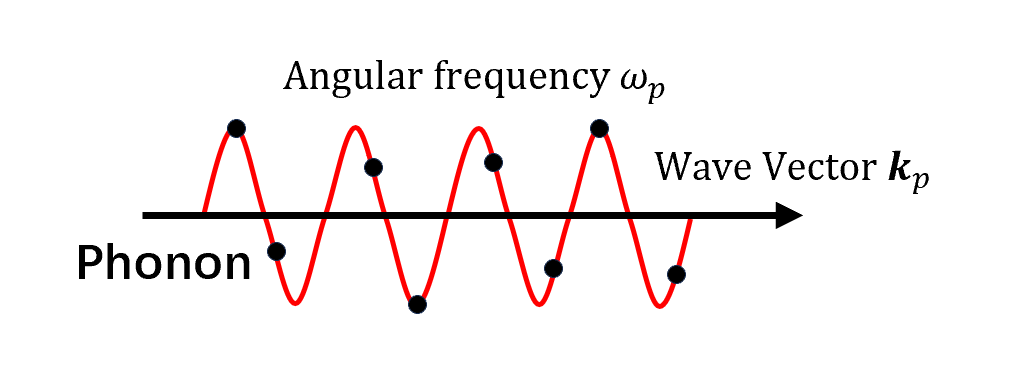
声子是刚性原子晶格中发生的量子化振动模式。
长波长声子的特性导致固体中产生声音，因此得名声子。
声子决定了材料的许多物理特性，包括热容量和热/电导率（声子的传播负责绝缘体中的热传导）。
在经典力学中，晶格的任何振动都可以分解为非局域简正振动模式的叠加。
当使用量子力学分析这些模式时，发现它们具有一些类似粒子的特性（波粒二象性）。因此，声子是一种准粒子。
当声子被视为粒子时，声子被称为玻色子，具有零自旋。声子能量 $E_p=\hbar\omega_p$ 是其势能和动能的总和，其中 $\hbar= h/2\pi$，$h$ 是普朗克常数。
声子有两种类型：声学声子，用 $A$ 表示，光学声子，用 $O$ 表示。
声学声子的频率随着波长的增加而变小，对应于晶格中的声波。纵向声子和横向声子通常分别缩写为 $LA$ 和 $TA$。
光学声子出现在一个晶胞含有多个原子的晶格中。它们之所以被称为光学的，是因为在离子晶体中很容易被光激发。光学声子通常缩写为 $LO$ 和 $TO$，分别表示纵向和横向类型。

电子

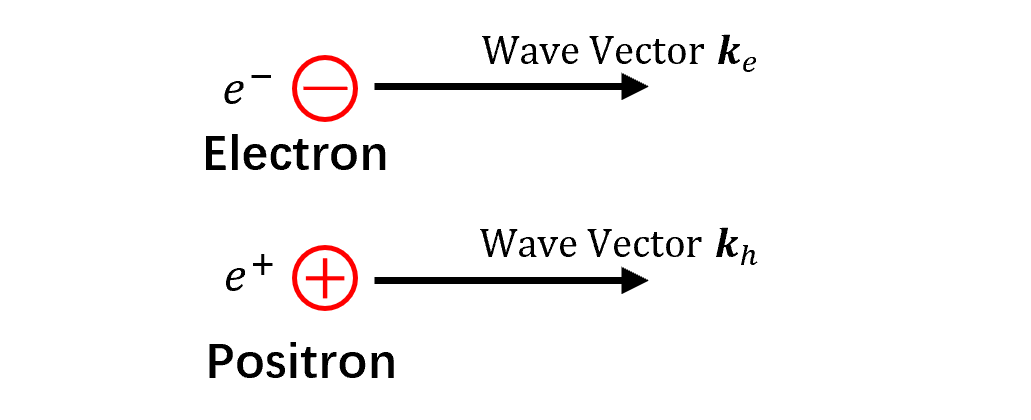
电子是带负电的亚原子粒子。电子的自旋为 $1/2$，是费米子。
电子的反粒子是正电子。正电子与电子具有相同数量的电荷、质量和自旋，只是电荷是相反的。
电子可以表现出粒子和波的特性，因此可以被视为准粒子。与原子核结合的电子表现为驻波，可以被观测到。
固体中的电子分为核心电子和外层电子。核心电子不参与键合，并且被认为始终与原子核一起移动。
外层电子距离原子核较远，又分为传导（或自由）电子和价电子。
在量子力学中，电子由狄拉克方程描述。
一般情况下，电子的能量分为势能（用键能表示）和动能（用速度表示）。

流体粒子

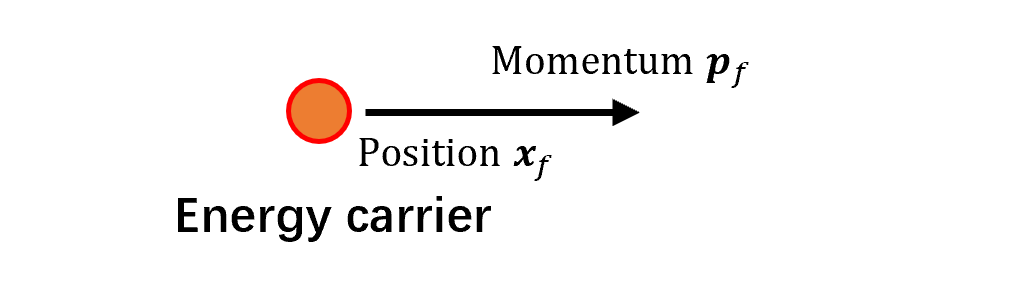
气体和液体由原子或分子（广义上称为流体粒子）组成。流体粒子可以是中性的或带电的，一直处于随机运动中。
流体粒子的能量分为势能、电子能和动能。
在理想气体中，气体粒子之间的碰撞是弹性的并且粒子之间的吸引力可以忽略不计。
对于理想气体，麦克斯韦-玻尔兹曼分布可以通过使用统计力学（以及能量分配和对称性的概念）来导出。
液体粒子具有足够的动能来拉伸粒子间吸引力，但不能完全克服它们（因此液体的密度接近固体）。当液体温度升高时，液体的速度增加。动能变大，以至于粒子克服了所有分子间力并自由移动，从而变成了气体。

光子

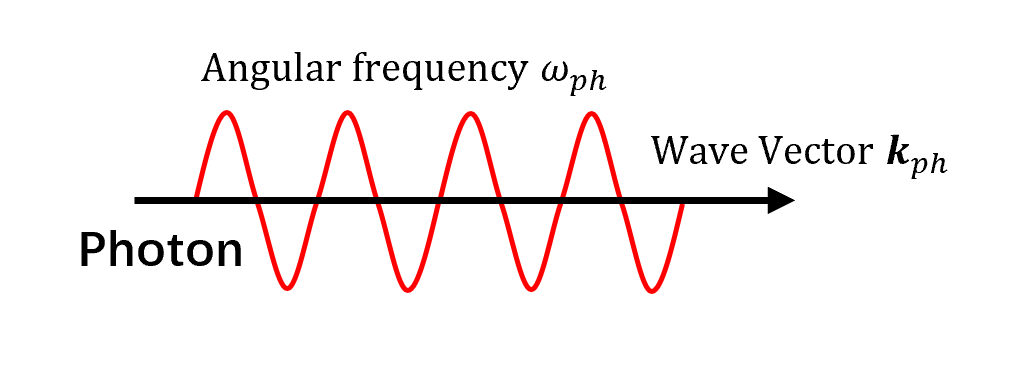
光子是电磁场激发的量子，也是量子电动力学中的基本粒子，是粒子物理学标准模型的一部分。
根据量子力学，光子具有波的特性。
光子的静止质量为零，但能量是确定且有限的。由于光子具有能量，广义相对论指出它们受到重力的影响。
光子的自旋为 1，是玻色子。单个光子由于其单位自旋而被圆偏振。
一般来说，电磁场由频率为 $f_{ph}$（角频率 $\omega_{ph}=2\pi f_{ph}$）、波长 $\lambda_{ph}$ 和速度 $u_{ph}$ 的平面单色波组成。
电磁波的量子特性由其能量 $E_{ph} = \hbar \omega_{ph}$ 给出。光子还具有动量 $\boldsymbol p_{ph} = \hbar \boldsymbol\kappa_{ph}$，其中 $\boldsymbol\kappa_{ph}$ 是波矢。
在真空中，光子的色散关系（角频率与波矢量之间的关系）是线性的，这个比例就是普朗克常数。
物质激发具有非线性色散关系，其动量与其能量不成正比。因此，这些粒子在真空中的传播速度比光速慢。

能量分布函数

在由多个粒子组成的系统中，观察到的宏观状态（系综平均值）通过每个微观状态存在的概率（能量分布函数）与每个粒子的微观状态（位置和动量）相关。

\[\left \langle \phi \right \rangle=\sum_if_i\phi_i\]

概率分布函数用于确定载流子能量及其传输特性。

这些粒子概率分布函数使我们能够描述晶格（声子）和电子比热容的温度依赖性、温度和气体动能之间的关系以及光子的黑体热发射。

平衡概率分布函数 $f_i^0$ 给出了零扰动下微观状态的最可能分布。

玻色-爱因斯坦分布 (声子，光子)

\[f_i^0 = \frac{1}{\exp(\frac{E_i}{k_\text BT})-1}\]

费米-狄拉克分布 (电子)

\[f_i^0 = \frac{1}{\exp(\frac{E_i-\mu}{k_\text BT})+1}\]

麦克斯韦-玻尔兹曼分布 (理想气体分子)

\[f_i^0 = \frac{1}{\exp(\frac{E_i}{k_\text BT})}\]

与平衡分布的偏差被用于这些载流子的输运性质，即玻尔兹曼输运理论。

粒子、波和准粒子

粒子

粒子是离散的。它们的能量集中在有明确边界的有限空间中。粒子存在于特定位置，为了到达空间中的不同点，粒子必须根据运动学定律移动。

粒子之间的相互作用遵循简单的定律，例如弹性碰撞情况下的能量和动量守恒定律。当没有相互作用时，粒子被称为弹道粒子。

波

波不能被视为有限实体。它们的能量分布在空间和时间上。波可以传播直到它存在于所有位置。可以分析波的相位以确定其在空间中的速度。波由频率和波长指定。

准粒子

准粒子（包括声子、电子和光子）同时具有粒子和波的性质，可以用波包来描述，即由许多不同波长的平面波叠加而成的能量局域化。

从某种意义上说，它们同时既是粒子又是波，这个概念被称为波粒二象性。

对于准粒子，粒子和波之间的经典区别可能变得模糊。它们的行为部分根据波动理论，部分根据粒子理论。

对传热物理学的贡献

热是能量的一种形式，表现为物质分子的运动，能够通过传导（通过声子、电子和流体粒子）、对流（通过流体粒子）和辐射（通过光子）从一个物体传递到另一个物体。

与热物理学最相关的物理学领域有：原子/分子动力学；固态（凝聚态）和流体态物理学; 电磁学; 量子光学。

玻尔兹曼提出：热容、熵和其他热力学性质是大量原子行为的结果，可以用力学和统计学来处理。他引入了玻尔兹曼常数 $k_B$，并与麦克斯韦一起提出了能量均分定律。
麦克斯韦创立了光的电磁理论，还对气体动力学理论、分子物理学和热力学做出了贡献。
普朗克发现能量以离散的形式存在，后来被称为“量子”。他假设允许物体吸收或发射的能量是有选择性的，必须为 $h\nu$ 的倍数，其中 $\nu$ 是光子频率。
玻耳在研究最简单的原子氢线谱时，假设原子只能吸收和发射对应于能级之间的能量差的量子能量。
泡利阐述了原子结构的规则（通常称为泡利不相容原理），单个原子中不能有两个或两个以上的电子处于完全相同的状态。
薛定谔方程描述了控制小粒子运动的概率波（或波函数）的形式，并指定了这些波如何受到外部影响的改变。这些波函数奠定了量子波力学的基础。
费米设计了一种计算遵循泡利不相容原理的粒子系统行为的方法，后来称为费米统计。狄拉克独立发展了等效理论。
Green 和 Kubo 发展了输运系数的波动耗散理论。
Ziman 对非平衡声子输运特性进行了变分处理。
Callaway 和 Holland 制定（并求解）了晶格热导率的单模弛豫时间模型。

基本常数和精细结构尺度

玻尔兹曼常数

\[k_\text B=1.38065\times10^{-23} ~ \text J/\text K\]

定义为能量载流子（声子、电子、光子或流体粒子）的平均热能与其绝对温度 $T$ 之间的关系。

当能量载流子被视为粒子时，该热能 $k_\text BT$ 用于归一化能量载流子的能量。

在统计力学中，$N$ 个粒子系统的熵 $S$ 定义为 $S=k_\text BN\ln Z$。这里，$Z$ 称为配分函数，它是描述系统在给定宏观约束的情况下可用能态分布的概率函数。

在动力学理论中，根据能量均分，为每个运动度分配一个等于 $k_\text BT/2$ 的能量。

普朗克常数

\[h=6.626069\times10^{−34} ~ \text J\cdot \text s\]

遵循量子力学，物体内的能量是其频率 $\nu$ 和 $h$ 的乘积。

约化的普朗克常数（也称为狄拉克常数）为 $\hbar = h/2\pi$。

普朗克常数用于描述量子化，主要能量载体的某些物理属性以固定量出现，而不是连续范围的值。

普朗克常数也出现在海森堡不确定性原理的陈述中，任何位置测量的不确定性 $\Delta x$ 和沿同一方向的动量测量的不确定性 $\Delta p_x$ 遵循关系 $\Delta p_x \Delta x \le \hbar/2$。

原子单位

四个基本常数，约化普朗克常数 $\hbar$、电子质量 $m_e$、库仑静电常数 $1/4\pi\varepsilon_0$（其中 $\varepsilon_0$ 是自由空间介电常数）和电子电荷 $e_c$ 用于定义原子单位。

原子长度：

\[r_\text B = \frac{4\pi\varepsilon_0\hbar^2}{m_e e_c^2}=5.2918\times 10^{-11}~ \text m\]

原子时间：

\[\tau_a=\frac{m_er_\text B^2}{\hbar} = 2.4189\times 10^{-17} ~ \text s\]

原子能量：

\[\frac{e_c^2}{4\pi\varepsilon_0r_\text B}=4.3597\times10^{-18}\text J=27.211~ \text{eV}\]

原子速度：

\[\frac{r_\text B}{\tau_a} = 2.1877 \times 10^6~ \text m/\text s\]

原子偶极矩：

\[e_cr_\text B=8.4783\times 10^{-30}~ \text C\cdot\text m\]

参考文献：

Kaviany M 《Heat Transfer Physics》 2008