声子蒙特卡罗模拟的理论基础
1. 玻尔兹曼输运方程
1.1 基于粒子玻尔兹曼输运方程:
\[\frac{\partial f}{\partial t} + \boldsymbol v_g(\omega,p)\nabla f = - \frac{f-f^{\text{loc}}}{\tau(\omega,p,T)}\]其中 $f=f(t,\boldsymbol x,\boldsymbol k,p)$ 是相空间中的声子分布函数,$\omega=\omega(\boldsymbol k,p)$ 是声子径向频率,$p$ 是声子极化,$T$ 是温度。此外,$f^\text{loc}$ 是由局部伪温度参数化的 BE 平衡分布。
使用声子束来代表模拟粒子:
\[f(t,\boldsymbol x,\boldsymbol k,p) \approx 8\pi^3N_\text{eff}\sum_i \delta^3(\boldsymbol x - \boldsymbol x_i) \delta^3(\boldsymbol k - \boldsymbol k_i) \delta_{p,p_i}\]$N_\text{eff}$ 是每个声子束中的声子有效数量。
1.2 基于能量玻尔兹曼输运方程 (energy-based BTE):
\[\frac{\partial e}{\partial t} + \boldsymbol v_g\nabla e = - \frac{e-e^{\text{loc}}}{\tau}\]这里,模拟粒子为能量 $e=\hbar\omega f$,且 $e^\text{loc}=\hbar\omega f^\text{loc}$。
\[e \approx 8\pi^3\varepsilon_\text{eff}\sum_i \delta^3(\boldsymbol x - \boldsymbol x_i) \delta^3(\boldsymbol k - \boldsymbol k_i) \delta_{p,p_i}\]其中 $\varepsilon_\text{eff}$ 定义为每个模拟粒子携带的有效能量 $\varepsilon_\text{eff}=N_\text{eff}\hbar\omega$。这里定义的能量粒子 $\varepsilon_\text{eff}$ 所代表的声子的有效数量是可变的。
1.3 基于偏差能量玻尔兹曼输运方程 (deviational energy-based BTE):
\[\frac{\partial e^d}{\partial t} + \boldsymbol v_g\nabla e^d = \frac{(e^{\text{loc}}-e^{\text{eq}}_{T_\text{eq}})-e^d}{\tau}\]其中,
\[e^{\text{eq}}_{T_\text{eq}}(\omega) = \frac{\hbar\omega}{\exp\left(\frac{\hbar\omega}{k_BT_\text{eq}}\right)-1}\]这里,模拟粒子为能量偏差:$e^d =e - e^{\text{eq}}{T\text{eq}}$。
\[e^d \approx 8\pi^3\varepsilon_\text{eff}^d\sum_i s(i) \delta^3(\boldsymbol x - \boldsymbol x_i) \delta^3(\boldsymbol k - \boldsymbol k_i) \delta_{p,p_i}\]$s(i)=+1$ 的粒子代表相对于参考状态增加的偏差能量份额(即较高温度区的“超额”声子群)。
$s(i)=-1$ 的粒子则代表相对于参考状态的负偏差能量份额(即较低温度区的“欠额”声子群)。
偏差能量方法通过引入参考平衡温度 $T_\text{eq}$,将计算聚焦于非平衡态的能量偏差,而不是完整的声子分布函数。这减少了计算中对大量平衡态声子的无效模拟,尤其在小温差或接近平衡态的情况下,显著提高了模拟效率。
偏差能量方法中,模拟粒子的数量和符号(正负)直接对应偏差能量的变化,减少了添加或删除粒子时可能引入的能量误差。同时,其计算机制天然遵循能量守恒原则。
2. 蒙特卡洛模拟算法
2.1 基于粒子模拟
初始化:
在初始温度 $T$ 下,使用 BE 统计计算体积 $V$ 中的声子数量:
\[N=V\int_{\omega=0}^{\omega_\text{max}}\sum_p D(\omega,p) f_T^\text{eq}(\omega) d\omega\]模拟粒子(每个代表一个声子束)的数量由 $N/N_\text{eff}$ 给出。
$N_\text{eff}$ 的值是通过平衡计算成本与获得具有统计意义的结果所需的粒子数量来确定的。
时间演化:
系统初始化后,将通过应用时间步长为 $\Delta t$ 的分割算法来进行模拟。 每一个时间步长由三个子步骤组成:
1). 声子 Drift
在此期间模拟粒子 $i$ 移动 $\boldsymbol v_{g,i}\Delta t$。
2). 采样
记录温度 ($T$) 和伪温度 ($T_\text{loc}$),它们是通过反转能量 ($E$) 和赝能量 ($\widetilde E$) 关系来计算的:
\[E=N_\text{eff}\sum_i\hbar\omega_i=V\int_{\omega=0}^{\omega_\text{max}}\sum_p \frac{D(\omega,p) \hbar\omega}{\exp\left(\frac{\hbar\omega}{k_BT}\right)-1} d\omega\] \[\widetilde E=N_\text{eff}\sum_i\frac{\hbar\omega_i}{\tau(\omega_i,p_i,T)}=V\int_{\omega=0}^{\omega_\text{max}}\sum_p \frac{D(\omega,p) \hbar\omega}{\tau(\omega,p,T)}\frac{1}{\exp\left(\frac{\hbar\omega}{k_BT_\text{loc}}\right)-1} d\omega\]温度 ($T$) 表示热平衡下的平均温度,伪温度 ($T_\text{loc}$) 与声子的散射过程有关,用于非平衡态下的声子行为分析。
3). 声子 Scatter
根据散射概率进行散射:
\[P_i = 1-\exp\left(-\frac{\Delta t}{\tau(\omega_i,p_i,T)}\right)\]散射通过采样新的频率、偏振和传播方向来完成。散射后的频率必须从分布 $D(\omega,p)f^\text{loc}/\tau(\omega,p,T)$ 中得出。
散射过程中要保证能量守恒。然而,由于散射声子的频率是随机采样的,因此需要添加或删除粒子,直到近似达到目标能量,强制实现能量守恒。
此方法并不总是确保能量守恒,导致模拟系统的能量随机游走,会引入确定性误差。
2.2 基于能量模拟
以能量作为模拟粒子,算法与上述类似,但需要做出以下调整:
- 初始化、边界发射或散射期间,频率分布的采样需考虑乘以因子 $\hbar\omega$ 的修正。
- 网格内能量的计算很简单,只需计算粒子的数量即可。 $N$ 个粒子的能量由 $\varepsilon_\text{eff} N$ 给出。
- 由于网格内的能量与粒子数量成正比,因此不需要添加或删除过程:只需保持粒子数量守恒,能量就严格自动守恒。
2.3 基于偏差能量模拟
初始化:
首先选择温度 $T_\text{eq}$ 下的平衡状态作为参考值。
如果初始状态 $f^0$ 与平衡分布相同,那么模拟开始时没有粒子。基于对温度偏差上限的猜测,系统的偏差能量可以估计为:
\[\Delta E = \int_{\omega=0}^{\omega_\text{max}}\sum_p\hbar\omega D(\omega,p)\times \bigg|\frac{1}{\exp(\frac{\hbar\omega}{k_BT})-1}-\frac{1}{\exp(\frac{\hbar\omega}{k_BT_\text{eq}})-1}\bigg| d\omega\]偏差有效能量 $\varepsilon_\text{eff}^d$ 可以根据所需的模拟粒子数量大致确定。
如果初始状态 $f^0$ 与平衡分布不同,则需要对粒子进行初始化。它们的频率和极化是从分布中得出的
\[D(\omega,p)e^d(\omega) = \hbar\omega D(\omega,p)\bigg[f^0-\frac{1}{\exp(\frac{\hbar\omega}{k_BT_\text{eq}})-1}\bigg]\]通常,$f^0$ 是某个温度 $T$ 下的平衡分布,由此上述表达式可简化为
\[D(\omega,p)e^d(\omega) = \hbar\omega D(\omega,p)\bigg[\frac{1}{\exp(\frac{\hbar\omega}{k_BT})-1}-\frac{1}{\exp(\frac{\hbar\omega}{k_BT_\text{eq}})-1}\bigg]\]如果 $T>T_\text{eq}$ 该函数为正,如果 $T < T_\text{eq}$ 该函数为负。因此,在后一种情况下,粒子被赋予负号。
频率的采样:通过将频率范围细分为 bin,根据上式定义一个离散化和归一化的累积分布,均匀地抽取一个0到1之间的随机数,通过该随机数对应归一化累积分布,从而找到对应的 bin。
时间演化:
(1) 声子 drift:
在这一时间步长 $\Delta t$,模拟粒子 $i$ 移动 $\boldsymbol v_{g,i}\Delta t$ 。
(2) 采样:
(a) 令 $C_j$ 为对应于时间 $t$ 时体积为 $V_j$ 的单元 $j$ 内的粒子的索引集。由于每个粒子代表相同的能量,因此偏差能量为
\[\Delta E_j = \varepsilon_\text{eff}^d \sum_{i\in C_j} s(i) = \varepsilon_\text{eff}^d (N_j^+-N_j^-)\]其中 $N^+_j$ 和 $N^−_j$ 分别是单元 $j$ 内正粒子和负粒子的数量。
(b) 相应的温度 $T_j$ 通过对下式进行数值反演来计算
\[\frac{\Delta E_j}{V_j} = \int_0^{\omega_\text{max}}\sum_p D(\omega,p)\hbar\omega \bigg[\frac{1}{\exp(\frac{\hbar\omega}{k_BT_j})-1} - \frac{1}{\exp(\frac{\hbar\omega}{k_BT_\text{eq}})-1} \bigg] d\omega\](c) 通过数值反演计算相应的伪温度 $[T_\text{loc}]_j$
\[\frac{\Delta \widetilde E_j}{V_j} = \int_0^{\omega_\text{max}}\sum_p \frac{D(\omega,p)\hbar\omega}{\tau(\omega,p,T_j)} \bigg[\frac{1}{\exp(\frac{\hbar\omega}{k_B[T_\text{loc}]_j})-1} - \frac{1}{\exp(\frac{\hbar\omega}{k_BT_\text{eq}})-1} \bigg] d\omega\] \[\Delta\widetilde E_j = \varepsilon^d_\text{eff} \sum_{i\in C_j}\frac{s(i)}{\tau(\omega_i,p_i,T_j)}\](3) 声子 scatter:
我们根据散射概率判断每个声子是否发生散射,散射概率公式为:
\[P(\omega_i, p_i, T_j) = 1 - \exp\left(-\frac{\Delta t}{\tau(\omega_i, p_i, T_j)}\right)\]其中,$\omega_i$ 是声子的频率,$p_i$ 是偏振,$\tau$ 是声子的散射时间,取决于频率、偏振和局部温度 $T_j$ 。
散射过程中,单元格 $j$ 中的声子群代表了一定的偏差能量:$E^d_\text{eff}(N^+{s,j} - N^-{s,j})$
其中:
- $N^+_{s,j}$ 表示单元格 $j$ 中正偏差粒子的数量;
- $N^-_{s,j}$ 表示单元格 $j$ 中负偏差粒子的数量。
散射后的声子群需要替换为新的粒子,其属性(频率和偏振)从以下分布中抽取:
\[\frac{D(\omega, p)(e^\text{loc} - e^\text{eq}_{T_\text{eq}})}{\tau(\omega, p, T_j)} = \frac{D(\omega, p)\hbar\omega}{\tau(\omega, p, T_j)} \bigg[\frac{1}{\exp\left(\frac{\hbar\omega}{k_B [T_\text{loc}]_j}\right) - 1} - \frac{1}{\exp\left(\frac{\hbar\omega}{k_B T_\text{eq}}\right) - 1} \bigg]\]3. 设置边界条件
在声子输运问题中,会出现各种类型的边界条件:绝热边界,等温边界,周期性边界。
3.1 绝热边界 (Adiabatic boundary)
绝热边界反映了所有入射声子。这种反射过程可分为两大类:漫反射和镜面反射。 在这两种情况下,假设声子反射时偏振和频率保持相同。
在此过程中唯一修改的参数是行进方向。
(i) 镜面反射保证能量守恒 \(e^d(\boldsymbol x, \boldsymbol k) = e^d(\boldsymbol x, \boldsymbol k')\) ,方向为:\(\boldsymbol k' = \boldsymbol k - 2(\boldsymbol k \cdot \boldsymbol n) \boldsymbol n\),其中 \(\boldsymbol n\) 为边界的法向量。
(ii) 漫反射相当于入射在边界上的声子的反射方向随机化,即与散射声子处理方式一致。
镜面反射发生在边界非常光滑时(相对于声子波长),即边界表面粗糙度远小于声子的波长。镜面反射不会导致声子分布的随机化,因此声子保持较强的方向性传输。
漫反射发生在边界粗糙度与声子波长相当或大于声子波长时。漫反射导致声子分布趋于各向同性,使声子传热效率降低。在纳米结构中,漫反射增强了声子边界散射效应,显著降低材料的有效热导率。
3.2 等温边界 (Isothermal boundary)
在温度 \(T_b\) 的等温边界条件下,入射到边界的声子会被边界完全吸收。同时,边界会以其自身温度 \(T_b\) 为准,从对应的平衡分布中重新发射声子。
每单位径向频率的发射热通量可以表示为:
\[q_{\omega,b}'' = \frac{1}{4} \sum_p \frac{D(\omega,p)v_g(\omega,p)\hbar\omega}{\exp\left(\frac{\hbar\omega}{k_B T_b}\right) - 1}\]在偏差能量模拟中,需要考虑等温边界与参考平衡温度 $T_\text{eq}$ 之间的热流差异,我们可以通过减去 \(T_\text{eq}\) 对应的热通量来得到修正的表达式:
\[q_{\omega,b}'' = \frac{1}{4} \sum_p D(\omega,p)v_g(\omega,p)\hbar\omega \cdot \bigg[\frac{1}{\exp\left(\frac{\hbar\omega}{k_B T_b}\right) - 1} - \frac{1}{\exp\left(\frac{\hbar\omega}{k_B T_\text{eq}}\right) - 1} \bigg]\]该公式提供了在等温边界条件下,发射粒子的频率分布函数。具体来说,它反映了边界在温度 \(T_b\) 下的非平衡声子输运特性,即边界如何根据温度差对声子进行吸收和重新发射。
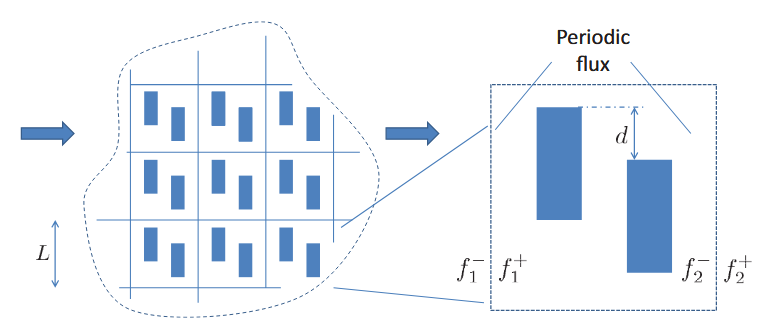
3.3 周期性边界 (Periodic boundary)
周期性边界条件允许我们仅通过考虑一个晶胞(周期)来有效模拟完整的结构。

在边界处,声子分布与局部平衡的偏差是周期性的,可以通过以下关系描述:
\[f_1^+ - f_{T_1}^\text{eq} = f_2^+ - f_{T_2}^\text{eq}\] \[f_1^- - f_{T_1}^\text{eq} = f_2^- - f_{T_2}^\text{eq}\]其中 $f_{T_1}^\text{eq}$ 和 $f_{T_2}^\text{eq}$ 指温度 $T_1$ 和 $T_2$ 下的平衡分布,上标 $+$ 表示粒子向右移动,上标 $-$ 表示粒子向左移动。该公式同时反映了热通量和温度梯度的周期性。
对于偏差能量分布,该关系变为
\[\hbar\omega(f_1^+ - f_{T_\text{eq}}^\text{eq} - f_{T_1}^\text{eq}) = \hbar\omega(f_2^+ - f_{T_\text{eq}}^\text{eq} - f_{T_2}^\text{eq})\] \[\hbar\omega(f_1^- - f_{T_\text{eq}}^\text{eq} - f_{T_1}^\text{eq}) = \hbar\omega(f_2^- - f_{T_\text{eq}}^\text{eq} - f_{T_2}^\text{eq})\]用偏差能量来表示为:
\[e_1^{d,+} - e_{T_1}^\text{eq} = e_2^{d,+} - e_{T_2}^\text{eq}\] \[e_1^{d,-} - e_{T_1}^\text{eq} = e_2^{d,-} - e_{T_2}^\text{eq}\]周期性边界条件可以通过以下方式强制实现:
(i) 将跨越周期性边界的粒子从系统的一侧移除,并重新插入到另一侧,同时保持粒子的属性不变。
(ii) 在边界生成新的粒子:这些粒子的行进方向在半球体上是随机的,在热边界,它们被发送到带有正号的右侧行进。相反,具有相同性质的负粒子从冷边界发射出来。粒子的生成遵循下列分布:
\[(e_{T_1}^\text{eq}-e_{T_2}^\text{eq})\frac{D(\omega,p)}{4\pi} v_g(\omega,p)\]参考文献:
[1] S. Mazumder, A. Majumdar, Monte Carlo Study of Phonon Transport in Solid Thin Films Including Dispersion and Polarization, Journal of Heat Transfer 123 (2001) 749–759.
[2] Q. Hao, G. Chen, M.-S. Jeng, Frequency-dependent Monte Carlo simulations of phonon transport in two-dimensional porous silicon with aligned pores, Journal of Applied Physics 106 (2009) 114321.
[3] J.-P.M. Péraud, N.G. Hadjiconstantinou, Efficient simulation of multidimensional phonon transport using energy-based variance-reduced Monte Carlo formulations, Phys. Rev. B 84 (2011) 205331.