态密度的数值求解方法
晶格动力学研究中最重要的量之一是态密度 (DOS),定义为在频率 $\omega$ 和 $\omega+d\omega$ 之间的简正模态的数量。
态密度的表达式:
\[\text{DOS}(\omega)=\frac{V}{8\pi^3}\sum_s\int\frac{dS_\omega}{|\Delta_{\boldsymbol k}\omega_s|}\]其中,$S_\omega$ 是等频面。
根采样法
这是一种最简单的方法 (也可称为直方图统计法)
\[\text{DOS}(\omega)=\frac{V}{8\pi^3}\sum_{\boldsymbol qs} \delta(\omega-\omega(\boldsymbol qs))\]根据此方法,我们可以统计位于 $\Delta\omega$ 中的模态数量,从而得到态密度。但该方法需要布里渊区内大量的 $\boldsymbol k$ 点(网格需要足够密)以得到准确的结果。
线性外推
GR 方法将第一布里渊区的不可约部分划分为由点 $\boldsymbol k_c$ 组成的均匀简单立方网格,点之间的距离为 \(2b\)。每个点 $\boldsymbol k_c$ 都位于一个小立方体的中心。从包含每个 $\boldsymbol k_c$ 的小立方体中提取 “所有” 频率,然后对所有立方体的贡献求和获得完整的频率分布。
在 $\boldsymbol k_c$ 处对应的特征频率为 $\omega(\boldsymbol k_c)$。我们假设线性外推法在每个小立方体中都适用,所以,等频面可以表示为垂直于 $\nabla\omega(\boldsymbol k_c)$ 的平行平面。两个这样的平行平面之间的体积元 $dV$ 与 $\omega$ 和 $\omega+d\omega$ 之间的频率数量成正比。当 $dV$ 接近 0 时,可以近似为
\[dV=Sdk_\perp\]其中 $S$ 是立方体限制的平面面积(即为截面积),$dk_\perp$ 是体积单元的厚度。
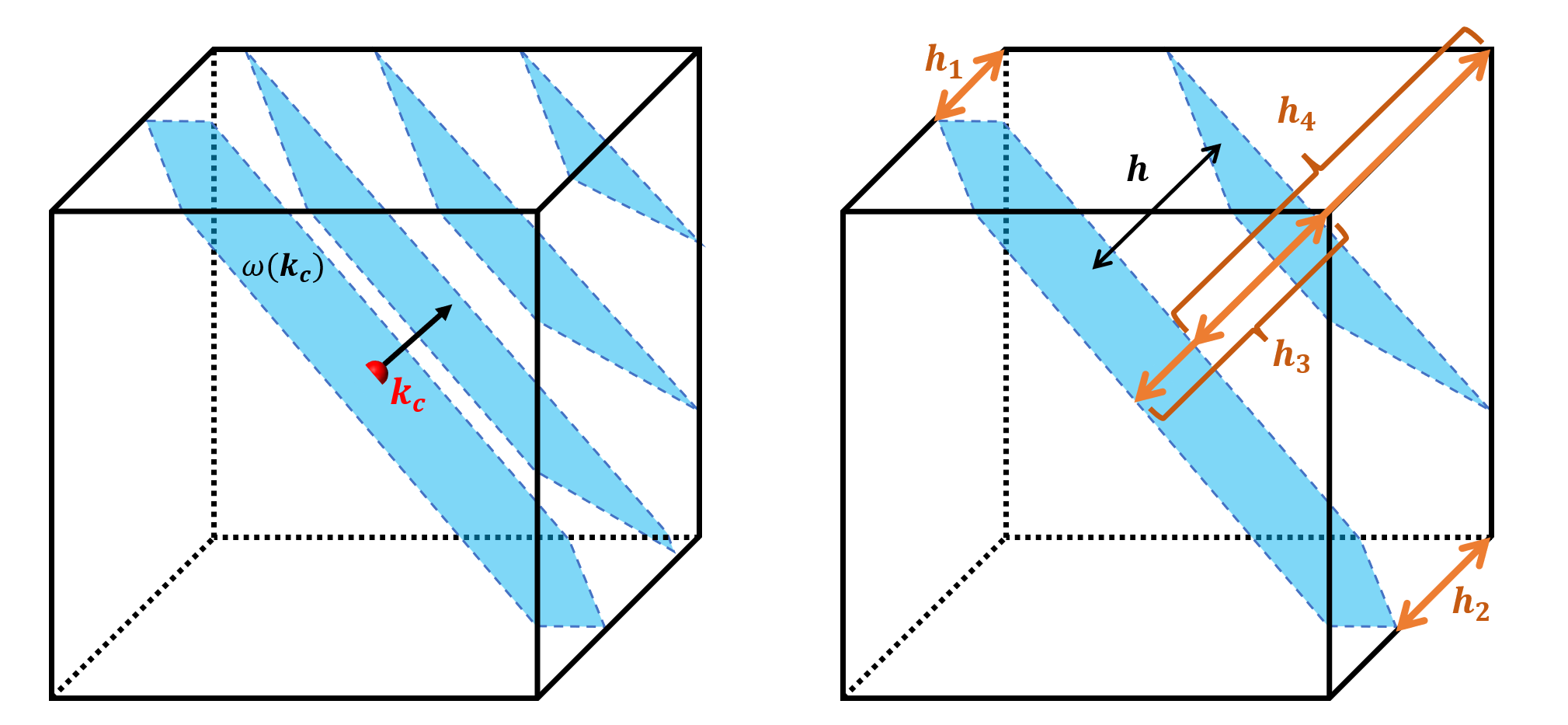
接下来需要考虑这一组恒频平面在立方体中横截面积的大小。首先假设等频平面的法线的三个方向余弦从大到小分别为 $l_1$,$l_2$ 和 $l_3$。
设任意截面与 $\boldsymbol k_c$ 的距离为 $h$,截面积表示为 $S(h)$
而且必然满足 $S(h) = S(-h)$, 所以我们只需考虑立方体的一半 ($h>0$)
以递增的顺序列出位于这半部分的四个角与通过立方体中心的平面的距离:
\(h_1 = b|l_1-l_2-l_3|\) \(h_2 = b(l_1-l_2+l_3)\) \(h_3 = b(l_1+l_2-l_3)\) \(h_4 = b(l_1+l_2+l_3)\)
在第一个范围 $(0\leq h \leq h_1)$ 中有两种可能性,取决于 $(l_1-l_2-l_3)$ 的符号。如果符号为正,则横截面是平行四边形,面积为
\[S(h) = 4b^2/l_1\]如果为负,则横截面为六边形,面积为
\[S(h) = \frac{2b^2(l_1l_2+l_2l_3+l_3l_1) - (h^2+b^2)}{l_1l_2l_3}\]在第二个范围 \((h_1\leq h \leq h_2)\) 中,形状是五边形,其面积为
\[S(h) = \frac{2b^2(l_1l_2+3l_2l_3+l_3l_1) - bh(-l_1+l_2+l_3) - \frac{1}{2}(h^2+b^2)}{l_1l_2l_3}\]在第三个范围 \((h_2\leq h \leq h_3)\) 中,形状是四边形,其面积为
\[S(h) = 2\frac{b^2l_3(l_1+l_2)-bhl_3}{l_1l_2l_3}\]在第四个范围 \((h_3\leq h \leq h_4)\) 中,形状是四边形,其面积为
\[S(h) = \frac{[b(l_1+l_2+l_3)-h]^2}{2l_1l_2l_3}\]这些表达式及其导数在各自的边界处都是连续的,\(S(h)\) 在整个范围内积分可得到立方体的体积。
对整个立方体进行线性外推可以获得频率变化
\[\Omega = \omega(\boldsymbol k_c) \pm h\nabla\omega(\boldsymbol k_c)\]其中 $0\leq h\leq h_4$
为了构造 $\text{DOS}(\omega)$,我们定义一个函数 $g_s(\boldsymbol k_c,\omega)$,它是通过线性外推整个以 $\boldsymbol k_c$ 为中心的立方体而获得的频率分布:
\[g_s(\boldsymbol k_c,\omega) = CW(\boldsymbol k_c)S_s(h)dh = CW(\boldsymbol k_c)S_s(w) \frac{d\omega}{|\nabla\omega(\boldsymbol k_c)|}\]其中, $\omega(\boldsymbol k_c) - h_4\nabla\omega(\boldsymbol k_c) \leq \omega \leq \omega(\boldsymbol k_c) + h_4\nabla\omega(\boldsymbol k_cs)$
这里 $C$ 是归一化常数,$W(\boldsymbol k_c)$ 是点 $\boldsymbol k_c$ 与对称性相关的权重因子
最后, 完整的态密度
\[\text{DOS}(\omega) = \sum_{\boldsymbol k_c, s} g_s(\boldsymbol k_c,\omega)\]GR 方法有两个实际困难: (i)它需要首先计算梯度 $\nabla\omega(\boldsymbol k_c)$, (ii)由于立方体通常不完全符合布里渊区,因此有必要确定区域不可约部分的立方体的统计权重。
线性外推的推广
GGR 方法的核心思想是使用仿射变换将平行六面体的布里渊区变换为立方体,从而使得原始 GR 方法可以用于任何格子。
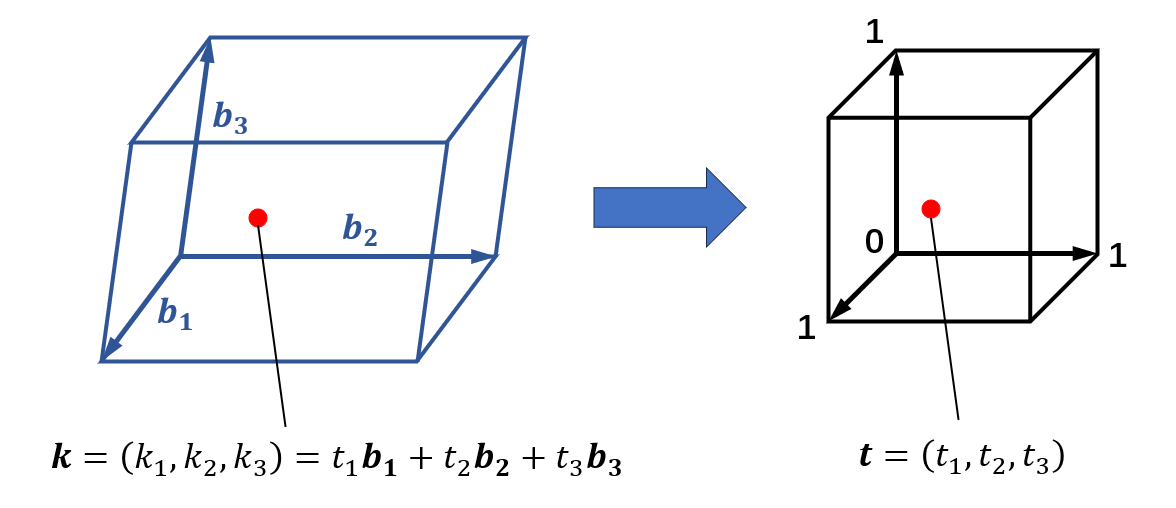
BZ是由三个倒易向量 $\boldsymbol b_i(i=1,2,3)$ 构成的平行六面体。$\boldsymbol k$ 点沿三个基向量 $\boldsymbol b_i$ 均匀分布。
仿射变换将平行六面体 BZ 的 $\boldsymbol k$ 基变为立方的 $\boldsymbol t=(t_1, t_2, t_3)$ 基:
\[\boldsymbol k = \boldsymbol b_1 t_1 + \boldsymbol b_2 t_2 + \boldsymbol b_3 t_3\]其中 $t_1, t_2, t_3 \in [0, 1]$
两组基底的体积元满足 $dV_k = \det(B)dV_t = \Omega dV_t$,其中 $\Omega$ 为 BZ 的体积。
我们将 $\text{DOS}(\omega)$(等频曲面 $S_\omega$ 上的积分)从 $\boldsymbol k$ 基变为立方的 $\boldsymbol t$ 基:
\[\text{DOS}(\omega)=\frac{1}{\Omega} \sum_s\int_{S_\omega}\frac{dS_k}{|\Delta_{\boldsymbol k}\omega_s|} = \sum_s\int_{S_\omega}\frac{dS_t}{|\Delta_{\boldsymbol t}\omega_s|}\]线性内插
将不可约部分内的立方体划分为多个等体积的四面体。在四面体的每个顶点处已知声子频率,然后四面体内部任意位置的声子频率 $\nabla\omega(\boldsymbol k)$ 可以通过线性内插得到
\[\omega(\boldsymbol k) = a_1\omega(\boldsymbol k_1) + a_2\omega(\boldsymbol k_2) + a_3\omega(\boldsymbol k_3) + a_4\omega(\boldsymbol k_4)\]其中,$a_i$ 是四面体的顶点权重系数,满足 $a_1+a_2+a_3+a_4 = 1$,而这些权重系数依赖于点 $\boldsymbol k$ 在四面体内的位置。
四面体法只需要粗网格下的 $\omega(\boldsymbol k_i)$ 的分布,不需要频率梯度(群速度)。
但是在带交叉处,即对简并性上的点进行采样,线性插值会导致误差增加。