Classical Kinetic Theory of Heat Conduction

Kinetic Theory of Gases

In classical kinetic theory, consider a molecule traveling a total path length $L$. The effective volume it sweeps out is $\pi d^2 L$, where $d$ is the molecular diameter. If the number density of the gas is $n$, then the number of molecules within this volume is $\pi n d^2 L$, meaning the number of collisions experienced is:

\[N = \pi n d^2 L\]

The mean free path $\Lambda$ between two collisions is then:

\[\Lambda = \frac{L}{N} = \frac{L}{\pi n d^2 L} = \frac{1}{n \sigma}\]

where $\sigma = \pi d^2$ is the collision cross-section.

Substituting the ideal gas relation $n = \frac{p}{k_B T}$ gives:

\[\Lambda = \frac{k_B T}{p \sigma}\]

To calculate the heat flux from a single molecule, assume its internal energy is $\varepsilon$, and its velocity component in the $x$ direction is $v_x$. Then the energy transfer per unit time is approximately:

\[q_x = \frac{1}{2} v_x \left[\varepsilon(x - \Lambda_x) - \varepsilon(x + \Lambda_x)\right]\]

Expanding using a Taylor series and neglecting higher-order terms:

\[q_x \approx -v_x \Lambda_x \frac{\mathrm{d} \varepsilon}{\mathrm{d}x} \approx -(\cos^2\theta) v \Lambda \frac{\mathrm{d} \varepsilon}{\mathrm{d}x}\]

Integrating over all directions (assuming isotropy), the total heat flux is:

\[q_x = -\frac{1}{2\pi} v \Lambda \frac{\mathrm{d} \varepsilon}{\mathrm{d}x} \left[\int_0^{2\pi} \mathrm{d}\varphi \int_0^{\pi/2} \cos^2\theta \sin\theta \, \mathrm{d}\theta \right] \frac{\mathrm{d} \varepsilon}{\mathrm{d}T} \frac{\mathrm{d}T}{\mathrm{d}x}\]

Which simplifies to:

\[q_x \approx -\frac{1}{3} C v \Lambda \frac{\mathrm{d}T}{\mathrm{d}x}\]

The resulting thermal conductivity is:

\[\lambda = \frac{1}{3} C v \Lambda\]

This shows that thermal conductivity is proportional to specific heat $C$, molecular speed $v$, and mean free path $\Lambda$.

Heat Conduction in Dielectrics

In dielectrics such as insulators or semiconductors, heat is carried by phonons, the quantized vibrations of the crystal lattice. Each phonon has energy $\hbar \omega$, where $\omega$ is the vibrational frequency.

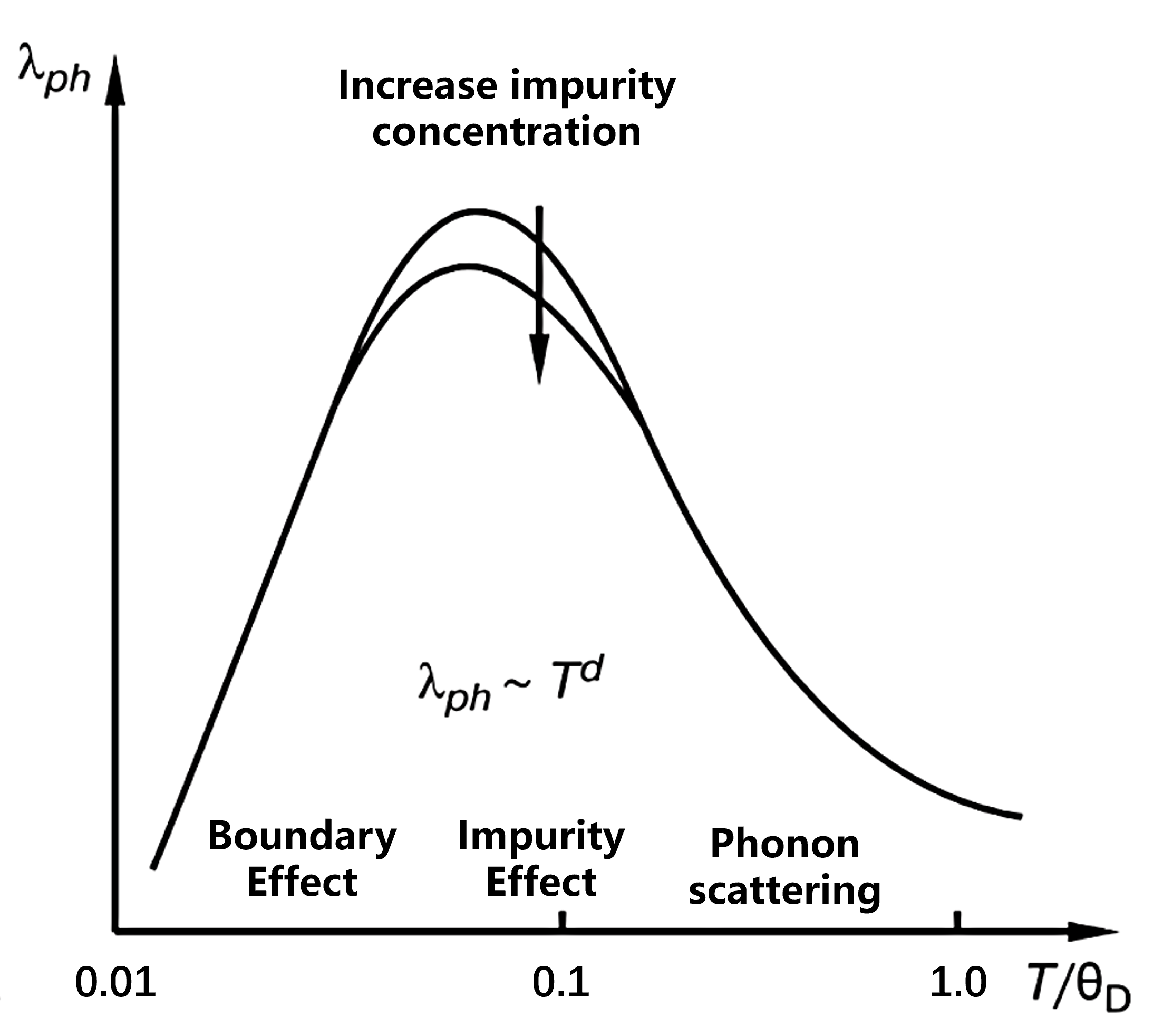
Phonon thermal conductivity is similarly given by:

\[\lambda_{ph} = \frac{1}{3} C_{ph} v_s \Lambda_{\Sigma}\]

where:

• $C_{ph}$ is the specific heat of the phonon system;
• $v_s$ is the effective sound speed;
• $\Lambda_{\Sigma}$ is the effective mean free path.

Main phonon scattering mechanisms include:

• Boundary scattering ($b$);
• Impurity scattering ($imp$);
• Phonon-phonon scattering ($ph$).

According to Matthiessen’s rule, the total inverse mean free path is the sum of the individual contributions:

\[\Lambda_{\Sigma}^{-1} = \Lambda_{ph}^{-1} + \Lambda_{imp}^{-1} + \Lambda_{b}^{-1}\]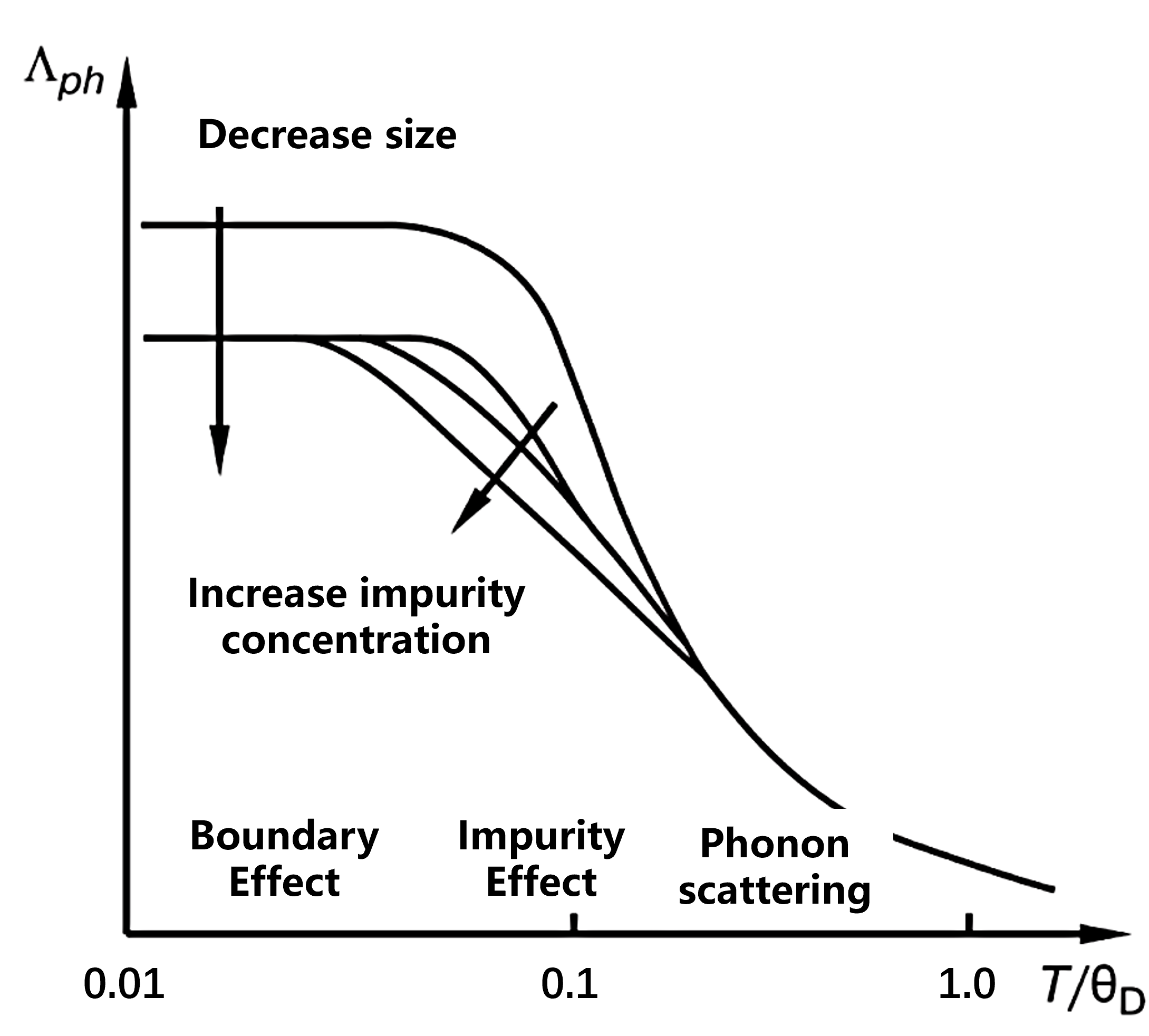

Heat Conduction in Metals

In metals, heat is mainly carried by free electrons. The thermal conductivity of the electron gas is:

\[\lambda_{e} = \frac{1}{3} C_{e} v_F \Lambda_{e}\]

where:

• $C_e$ is the electronic specific heat;
• $v_F$ is the Fermi velocity;
• $\Lambda_e$ is the mean free path of electrons.

Again using Matthiessen’s rule:

\[\frac{1}{\Lambda_e} = \frac{1}{\Lambda_{ph}} + \frac{1}{\Lambda_d} + \frac{1}{\Lambda_b}\]

Boltzmann Transport Equation

At the microscopic level, heat transport is described by particle distribution functions. In equilibrium, these are:

• Maxwell–Boltzmann distribution (classical gases);
• Bose–Einstein distribution (e.g., phonons);
• Fermi–Dirac distribution (e.g., electrons).

When far from equilibrium, the distribution becomes $f(\vec{r}, \vec{p}, t)$ and evolves according to the Boltzmann transport equation:

\[\frac{\partial f}{\partial t} + \vec v \cdot \nabla_{\vec r} f + \vec F \cdot \nabla_{\vec p} f = \left(\frac{\partial f}{\partial t}\right)_\text{st}\]

where the right-hand collision term $\left(\partial f / \partial t\right)_{\text{st}}$ describes how the system relaxes toward equilibrium.

Fourier Equation

At the macroscopic level, classical Fourier’s law governs steady-state heat conduction:

\[\vec q = -\lambda \nabla T\]

Substituting into energy conservation gives the heat diffusion equation:

\[\rho C_p \frac{\partial T}{\partial t} = -\nabla \cdot \vec q\]

Which becomes:

\[\rho C_p \frac{\partial T}{\partial t} = \lambda \nabla^2 T \quad \Rightarrow \quad \frac{\partial T}{\partial t} = a \nabla^2 T\]

Here, $a = \frac{\lambda}{\rho C_p}$ is the thermal diffusivity, describing how temperature disturbances propagate in the medium.

Summary

• Thermal transport depends not only on intrinsic properties like specific heat, velocity, and mean free path, but also on the characteristic size and timescale.
• When the system size is smaller than the mean free path, Fourier’s law fails; one should apply the Boltzmann equation or molecular dynamics.
• When the system size is comparable to carrier wavelengths, wave effects dominate and require wave-based models (e.g., phonon interference or localization theory).