Dispersion Relations of Elastic Waves in Plates
This article studies wave propagation by solving the elastic equation in a continuous medium.
In a plate, waves can be classified into longitudinal (P) waves and transverse (S) waves. S waves further include SH and SV waves.
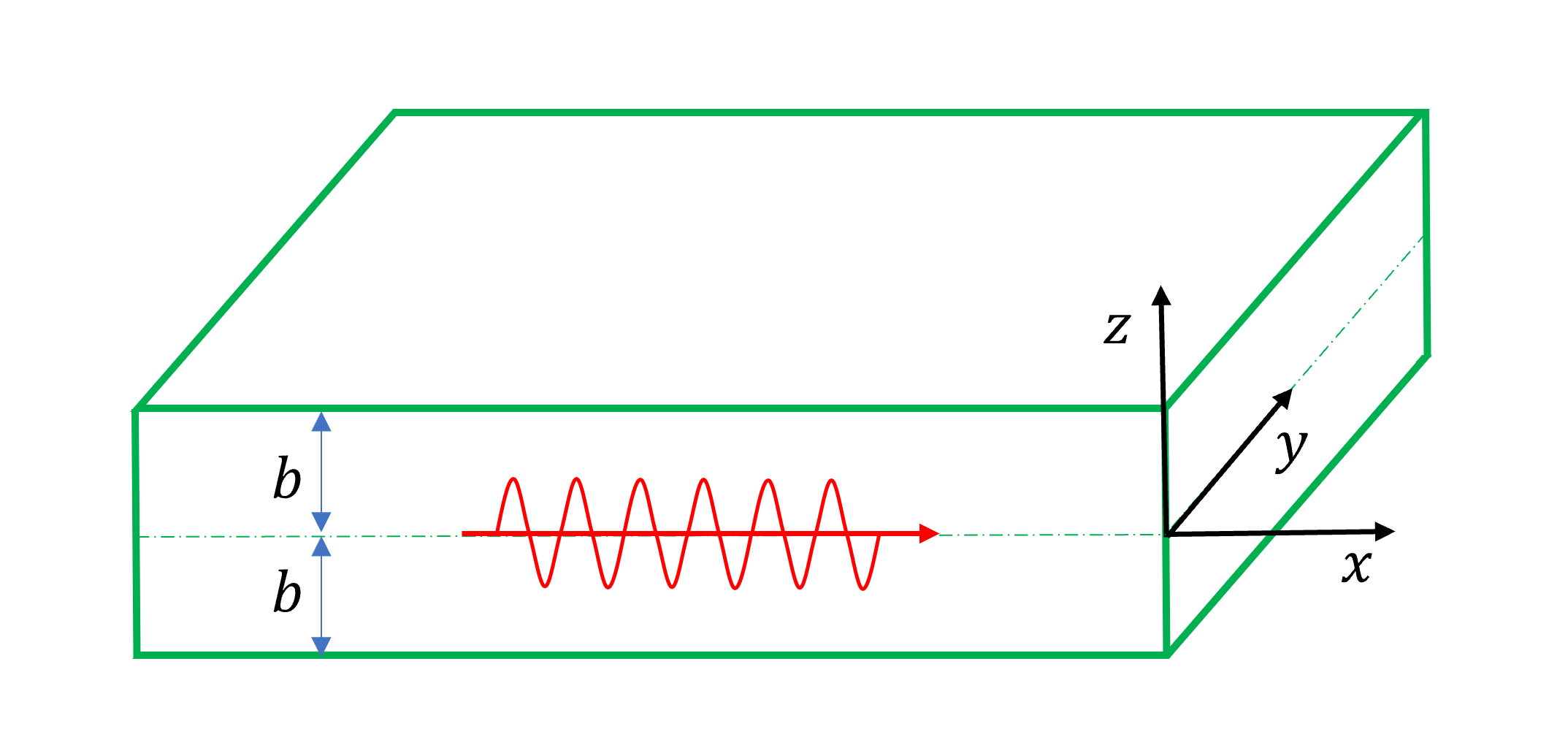
Assume the wave propagates along the $x$-axis. If particle motion is in $x$, it is a P wave; in $y$, an SH wave; in $z$, an SV wave.
SV and P waves couple under stress-free boundary conditions to form Rayleigh-Lamb waves.
Elastic Wave Equation
In the continuous medium approximation, the wave equation for propagation along $x$ is:
\[\mu \Delta \vec{u} + (\lambda + \mu) \nabla (\nabla \cdot \vec{u}) = \rho \frac{\partial^2 \vec{u}}{\partial t^2}\]Here, $\vec{u}$ is the displacement vector; $\lambda$, $\mu$ are Lamé constants; $\rho$ is the density.
All solutions can be written using scalar and vector potentials:
\[\vec{u} = \nabla \varphi + \nabla \times \vec{\psi}\]Dispersion Relation of SH Waves
For SH waves: $\vec{u} = (0, u_y, 0)$.
Wave equation:
\[\frac{\partial^2 u_y}{\partial x^2} + \frac{\partial^2 u_y}{\partial z^2} = \frac{1}{c_t^2} \frac{\partial^2 u_y}{\partial t^2}\]with $c_t = \sqrt{\mu / \rho}$.
Solution:
\[u_y = (A_1 \sin \beta z + A_2 \cos \beta z) e^{i(\xi x - \omega t)}\]where:
\[\beta^2 + \xi^2 = \frac{\omega^2}{c_t^2}\]Boundary condition at $y = \pm b$:
\[\tau_{zy} = \mu \frac{\partial u_y}{\partial z} = 0\]From the boundary condition:
\[\cos \beta b \sin \beta b = 0 \quad \Rightarrow \quad \beta b = \frac{n\pi}{2}, \quad n = 0,1,2,...\]Dispersion relation:
\[\omega^2 = c_t^2 \left[ \xi^2 + \left( \frac{n\pi}{2b} \right)^2 \right]\]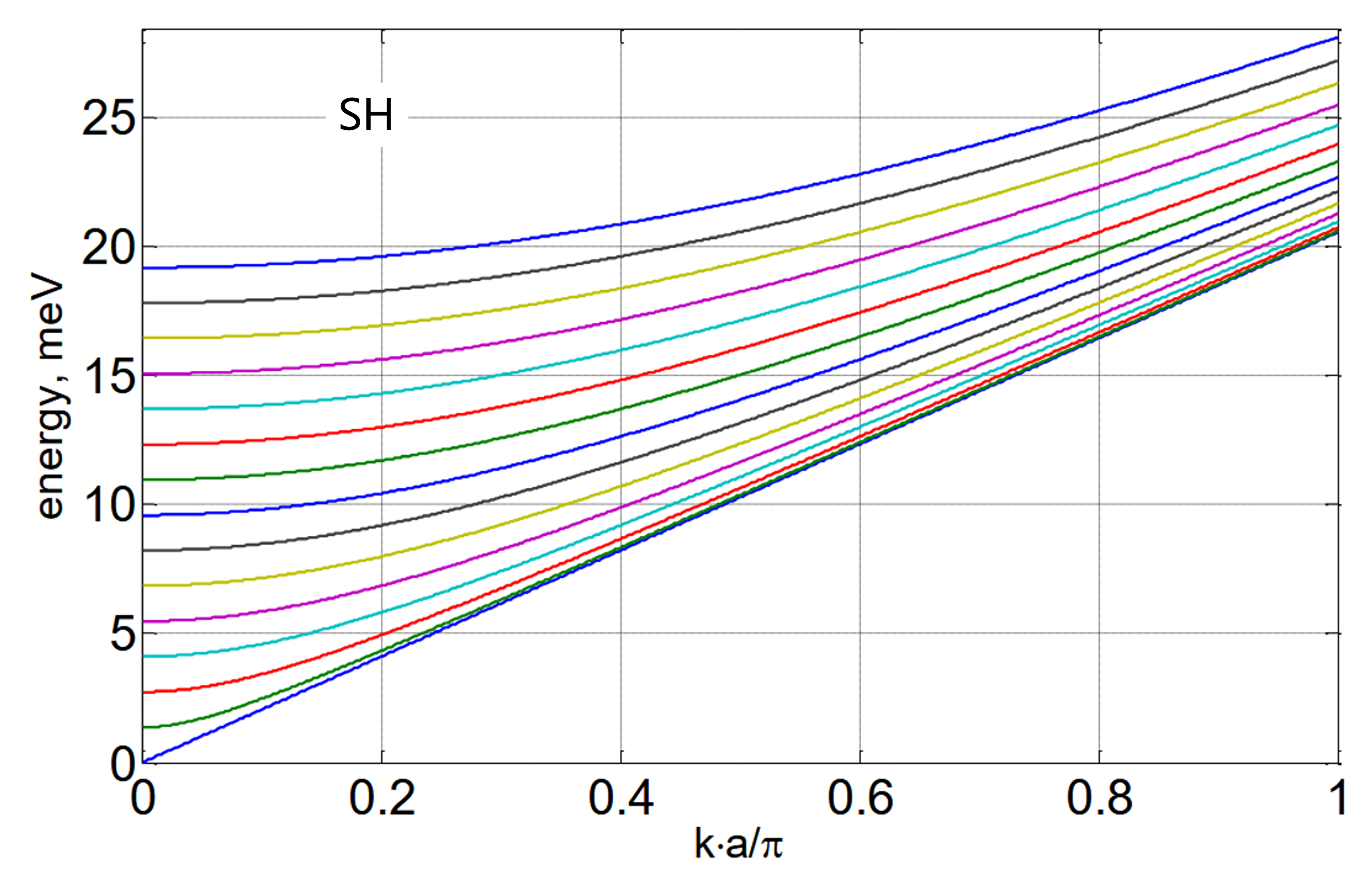
Dispersion Relation of Rayleigh-Lamb Waves
Consider a plate of thickness $2b$ with stress-free boundaries, where both P and SV waves exist.
Displacement: $\vec{u} = (u_x, 0, u_z)$, scalar potential: $\varphi$, vector potential: $\vec{\psi} = (0, \psi_y, 0)$.
Wave equations:
\[\nabla^2 \varphi = \frac{1}{c_l^2} \frac{\partial^2 \varphi}{\partial t^2}, \quad \nabla^2 \psi_y = \frac{1}{c_t^2} \frac{\partial^2 \psi_y}{\partial t^2}\]with $c_l = \sqrt{(\lambda + 2\mu)/\rho}$.
The solutions are:
\[\varphi=(A\sin\alpha z+B\cos\alpha z)e^{i(\xi x-\omega t)}\] \[\psi_y=i(C\sin\beta z+ D\cos\beta z)e^{i(\xi x-\omega t)}\]Symmetric and antisymmetric waves are treated separately.
Symmetric Waves
For symmetric waves ($A=D=0$):
\[\frac{\tan\beta b}{\tan\alpha b} = -\frac{4\alpha\beta \xi^2}{(\xi^2-\beta^2)^2}\]Antisymmetric Waves
For antisymmetric waves ($B=C=0$):
\[\frac{\tan\beta b}{\tan\alpha b} = -\frac{(\xi^2-\beta^2)^2}{4\alpha\beta \xi^2}\]Rayleigh-Lamb Frequency Equation
Combining symmetric and antisymmetric cases:
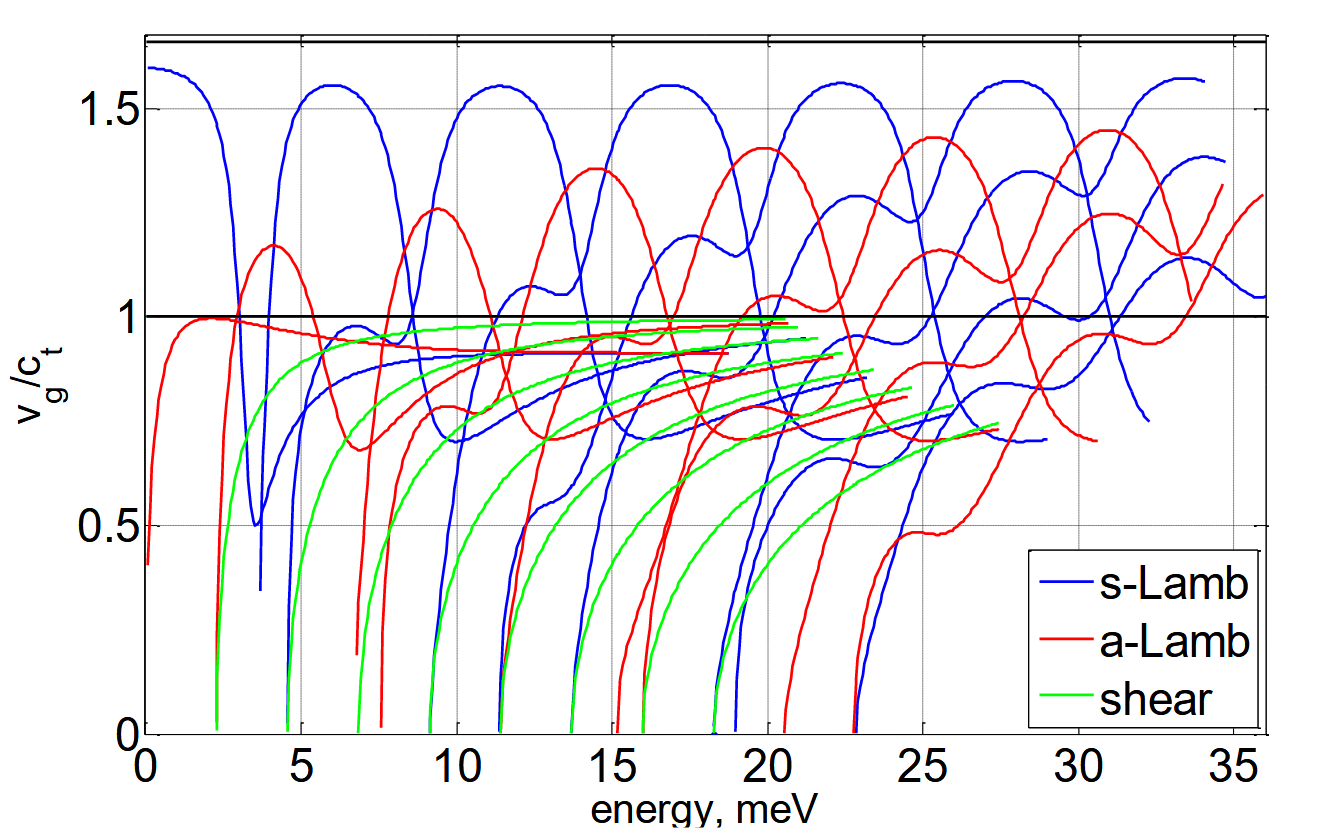
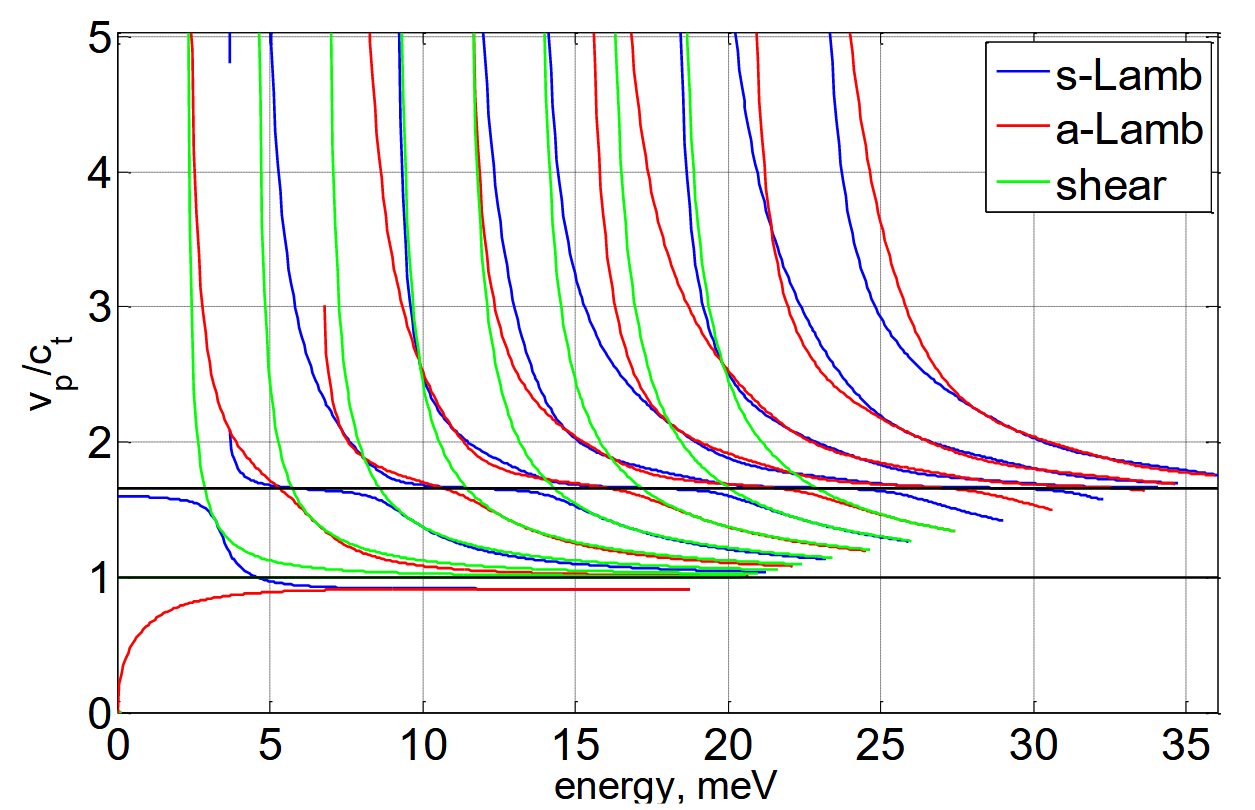
\[F(\alpha,\beta,\xi) = \frac{\tan\beta b}{\tan\alpha b} + \left(\frac{4\alpha\beta \xi^2}{(\xi^2-\beta^2)^2}\right)^{\pm 1} = 0\]Group Velocity and Phase Velocity
The phase velocity is the propagation velocity of the wave phase:
\[v_p=\frac{\omega}{k}\]The group velocity is the velocity at which energy is transmitted in the medium:
\[v_g=\frac{\partial\omega}{\partial k}\]