Dispersion Relations of Elastic Waves in Rods
Elastic Equation in Rods
General equation for elastic wave propagation:
\[\mu \nabla^2 \vec{u} + (\lambda + \mu) \nabla (\nabla \cdot \vec{u}) = \rho \frac{\partial^2 \vec{u}}{\partial t^2}\]Here, $\vec{u}$ is the displacement vector; $\lambda$, $\mu$ are Lamé constants characterizing the elasticity; $\rho$ is the density; $t$ is time.
Express $\vec{u}$ as a combination of scalar potential $\varphi$ and vector potential $\vec{\psi}$:
\[\vec{u} = \nabla \varphi + \nabla \times \vec{\psi}\]Substituting into the wave equation:
\[\nabla^2 \varphi = \frac{1}{c_l^2} \frac{\partial^2 \varphi}{\partial t^2}, \quad \nabla^2 \vec{\psi} = \frac{1}{c_t^2} \frac{\partial^2 \vec{\psi}}{\partial t^2}\]where $c_l = \sqrt{(\lambda + 2\mu)/\rho}$ is the longitudinal wave speed and $c_t = \sqrt{\mu/\rho}$ is the shear wave speed.
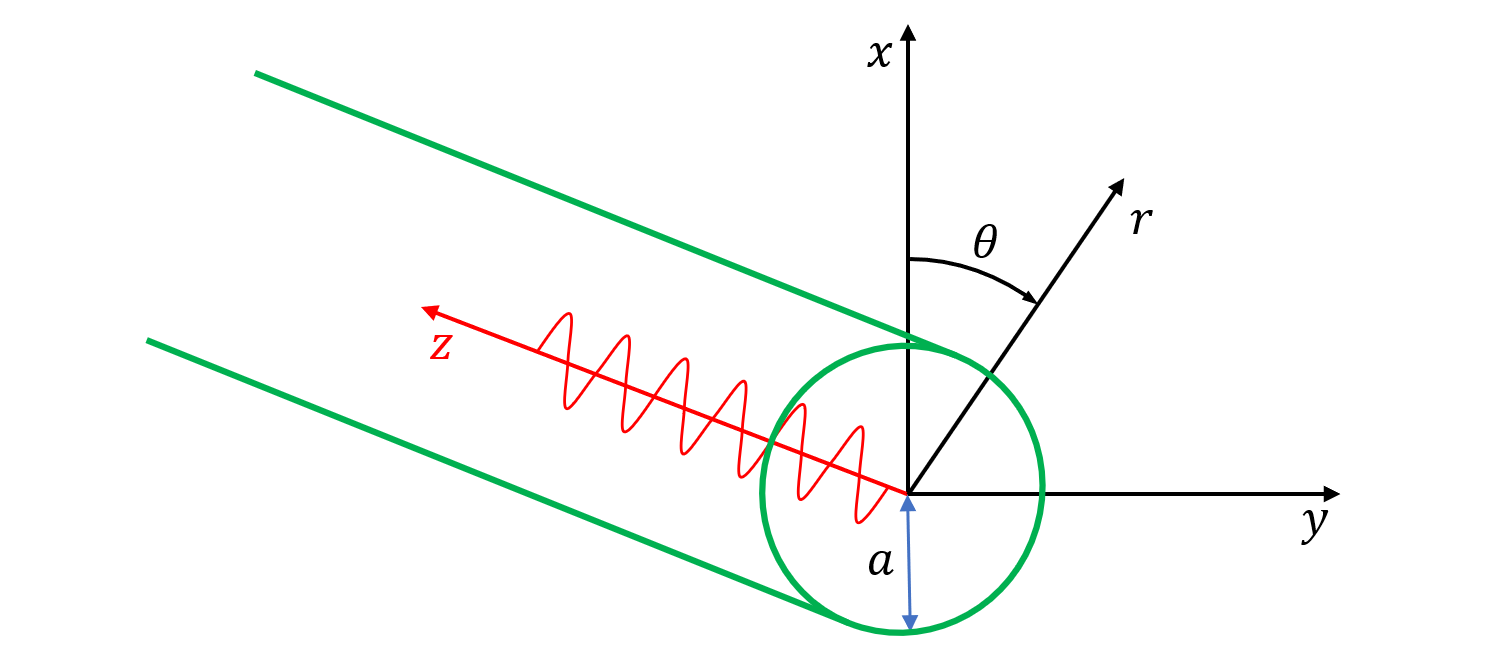
In cylindrical coordinates, the displacement components are:
\[u_r = \frac{\partial \varphi}{\partial r} + \frac{1}{r} \frac{\partial \psi_z}{\partial \theta} - \frac{\partial \psi_\theta}{\partial z}\] \[u_\theta = \frac{1}{r} \frac{\partial \varphi}{\partial \theta} + \frac{\partial \psi_r}{\partial z} - \frac{\partial \psi_z}{\partial r}\] \[u_z = \frac{\partial \varphi}{\partial z} + \frac{1}{r} \frac{\partial (\psi_\theta r)}{\partial r} - \frac{1}{r} \frac{\partial \psi_r}{\partial \theta}\]Stress components:
\[\tau_{rr} = \lambda\left(\frac{\partial u_r}{\partial r} + \frac{u_r}{r} + \frac{1}{r} \frac{\partial u_\theta}{\partial \theta} + \frac{\partial u_z}{\partial z} \right) + 2\mu \frac{\partial u_r}{\partial r}\] \[\tau_{r\theta} = \mu \left( \frac{\partial u_\theta}{\partial r} - \frac{u_\theta}{r} + \frac{1}{r} \frac{\partial u_r}{\partial \theta} \right)\] \[\tau_{rz} = \mu \left( \frac{\partial u_r}{\partial z} + \frac{\partial u_z}{\partial r} \right)\]Consider an infinitely long solid rod of radius $a$. Assume stress-free boundary conditions on the surface:
\[\tau_{rr} = \tau_{r\theta} = \tau_{rz} = 0, \quad r = a\]Torsional Waves

Torsional waves have only an angular displacement component $u_\theta$:
\[u_\theta = \frac{1}{\beta} B J_1(\beta r) \exp[i(\xi z - \omega t)]\]The frequency equation under boundary conditions:
\[\beta a \cdot J_0(\beta a) - 2 J_1(\beta a) = 0\]Dispersion relation:
\[\omega^2 = c_t^2 (\xi^2 + \beta^2)\]Define nondimensional quantities $\overline{\beta} = \beta a$, $\overline{\xi} = \xi a$, and $\Omega = \omega a / c_t$, then:
\[\Omega^2 = \overline{\xi}^2 + \overline{\beta}^2\]Longitudinal Waves
Longitudinal waves are axisymmetric, with radial $u_r$ and axial $u_z$ displacement:
\[u_r = [-\alpha A J_1(\alpha r) - i\xi C J_1(\beta r)] \exp[i(\xi z - \omega t)]\] \[u_z = [i\xi A J_0(\alpha r) + \beta C J_0(\beta r)] \exp[i(\xi z - \omega t)]\]Frequency equation:
\[(\xi^2 - \beta^2)^2 \frac{(\alpha a) J_0(\alpha a)}{J_1(\alpha a)} + 4\xi^2 \alpha^2 \frac{(\beta a) J_0(\beta a)}{J_1(\beta a)} = 2\alpha^2 (\xi^2 + \beta^2)\]Dispersion relation:
\[\omega^2 = c_t^2 (\xi^2 + \beta^2) = c_l^2 (\xi^2 + \alpha^2)\]In nondimensional form:
\[\Omega^2 = \overline{\xi}^2 + \overline{\beta}^2 = \left(\frac{c_l}{c_t}\right)^2 (\overline{\xi}^2 + \overline{\alpha}^2)\]Flexural Waves
For flexural waves, all three displacement components must be considered:
\[u_r=\left[A\frac{\partial}{\partial r}J_1(\alpha r)+\frac{B}{r}J_1(\beta r)+ikCJ_2(\beta r)\right]\cos(\theta)\exp[i(\xi z-\omega t)]\] \[u_\theta=\left[-\frac{A}{r}J_1(\alpha r)+ikCJ_2(\beta r)-B\frac{\partial}{\partial r}J_1(\beta r)\right]\cos(\theta)\exp[i(\xi z-\omega t)]\] \[u_z=\left[ikAJ_1(\alpha r)-\frac{C}{r}\frac{\partial}{\partial r}[rJ_2(\beta r)]-\frac{C}{r}J_2(\beta r)\right]\cos(\theta)\exp[i(\xi z-\omega t)]\]From the boundary conditions, the frequency equation for flexural waves is:
\[J_1(\overline\alpha)J_1^2(\overline\beta) \begin{vmatrix} \overline\xi^2-\overline\beta^2+4-2\Psi_\alpha & 2\overline\xi(\overline\beta^2-2+\Psi_\beta) & 2\Psi_\beta-4 \\ 4-2\Psi_\alpha & 2\overline\xi(\Psi_\beta-2) & \overline\beta^2-4+2\Psi_\beta \\ 2\overline\xi(\Psi_\alpha-1) & (\overline\beta^2-\overline\xi^2)(\Psi_\beta-1) & \overline\xi \end{vmatrix} =0\] \[\Psi_\alpha = \overline\alpha J_0(\overline\alpha)/J_1(\overline\alpha)\] \[\Psi_\beta = \overline\beta J_0(\overline\beta)/J_1(\overline\beta)\]Non-dimensional dispersion relation:
\[\Omega^2=\overline\xi^2+\overline\beta^2 = (c_l/c_t)^2(\overline\xi^2+\overline\alpha^2)\]Numerical Solution
Depending on whether $\alpha$ is real or imaginary, the solutions can be divided into two regions:
Region I: $\omega > c_l\xi$, $\alpha$ is real.
Region II: $\omega < c_l\xi$, $\alpha$ is imaginary, replaced by $i\alpha’$ (where $\alpha’^2 = -\alpha^2$).
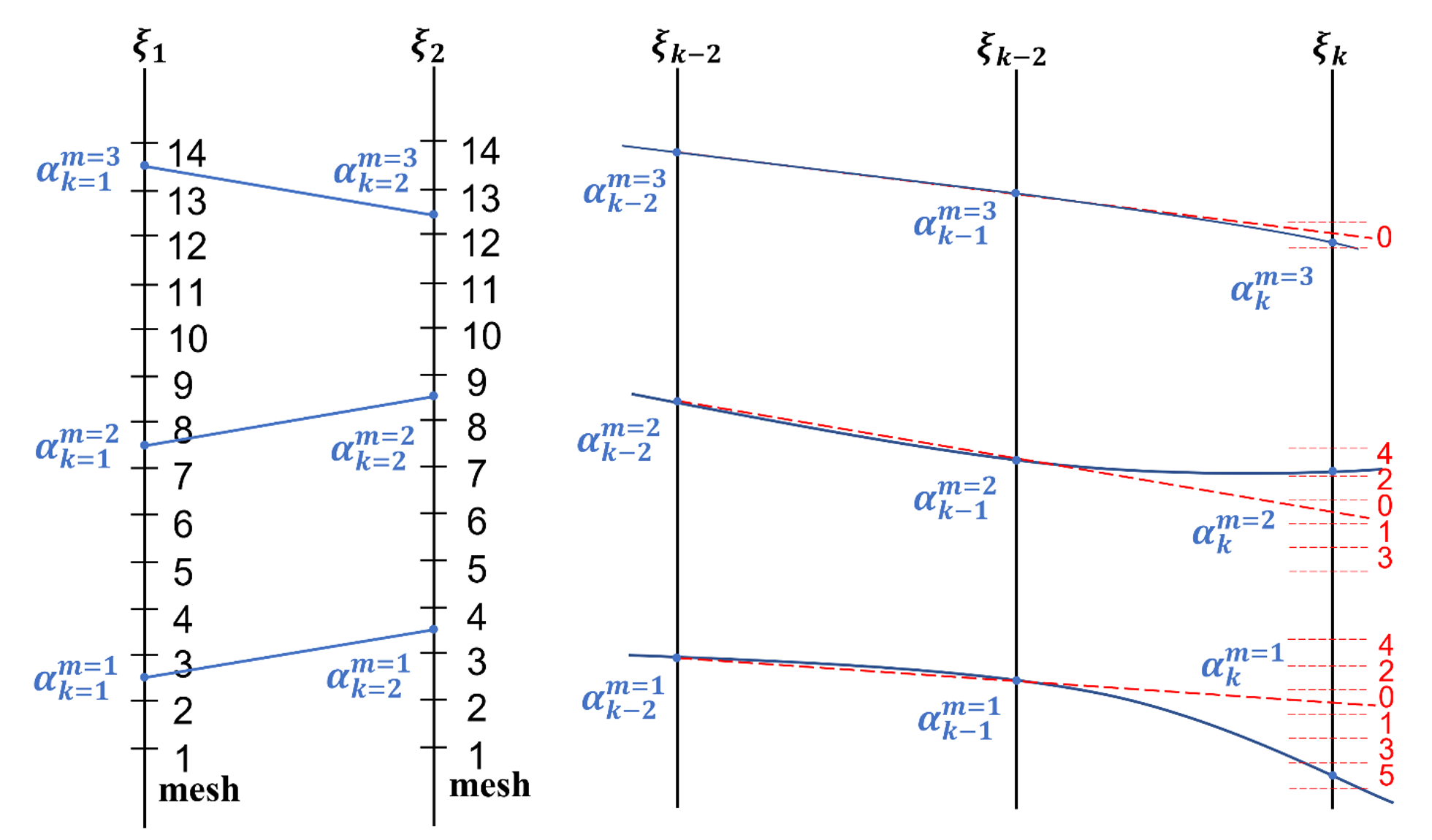
For different regions, the following root-finding method is used:
-
At the smallest wavenumber, two sets of roots are determined by sweeping.
-
Based on the initial roots, the equation is solved layer by layer using an adaptive approach.