Theoretical framework for phonon Monte Carlo simulations
1. Boltzmann Transport Equation
1.1 Particle-Based Boltzmann Transport Equation:
\[\frac{\partial f}{\partial t} + \boldsymbol v_g(\omega,p)\nabla f = - \frac{f-f^{\text{loc}}}{\tau(\omega,p,T)}\]where $f=f(t,\boldsymbol x,\boldsymbol k,p)$ is the phonon distribution function in phase space, $\omega=\omega(\boldsymbol k,p)$ is the phonon angular frequency, $p$ is phonon polarization, and $T$ is temperature. Moreover, $f^\text{loc}$ is the BE equilibrium distribution parameterized by a local pseudo-temperature.
Using phonon bundles to represent simulated particles:
\[f(t,\boldsymbol x,\boldsymbol k,p) \approx 8\pi^3N_\text{eff}\sum_i \delta^3(\boldsymbol x - \boldsymbol x_i) \delta^3(\boldsymbol k - \boldsymbol k_i) \delta_{p,p_i}\]where $N_\text{eff}$ is the effective number of phonons in each phonon bundle.
1.2 Energy-Based Boltzmann Transport Equation (Energy-Based BTE):
\[\frac{\partial e}{\partial t} + \boldsymbol v_g\nabla e = - \frac{e-e^{\text{loc}}}{\tau}\]Here, simulated particles represent energy $e=\hbar\omega f$, and $e^\text{loc}=\hbar\omega f^\text{loc}$.
\[e \approx 8\pi^3\varepsilon_\text{eff}\sum_i \delta^3(\boldsymbol x - \boldsymbol x_i) \delta^3(\boldsymbol k - \boldsymbol k_i) \delta_{p,p_i}\]where $\varepsilon_\text{eff}$ is defined as the effective energy carried by each simulated particle, $\varepsilon_\text{eff}=N_\text{eff}\hbar\omega$. The effective number of phonons represented by the energy particle $\varepsilon_\text{eff}$ is variable.
1.3 Deviational Energy-Based Boltzmann Transport Equation (Deviational Energy-Based BTE):
\[\frac{\partial e^d}{\partial t} + \boldsymbol v_g\nabla e^d = \frac{(e^{\text{loc}}-e^{\text{eq}}_{T_\text{eq}})-e^d}{\tau}\]where,
\[e^{\text{eq}}_{T_\text{eq}}(\omega) = \frac{\hbar\omega}{\exp\left(\frac{\hbar\omega}{k_BT_\text{eq}}\right)-1}\]Here, simulated particles represent deviational energy: $e^d = e - e^{\text{eq}}{T\text{eq}}$.
\[e^d \approx 8\pi^3\varepsilon_\text{eff}^d\sum_i s(i) \delta^3(\boldsymbol x - \boldsymbol x_i) \delta^3(\boldsymbol k - \boldsymbol k_i) \delta_{p,p_i}\]$s(i)=+1$ represents a share of deviational energy increase relative to the reference state (the “excess” phonon group in higher-temperature regions).
$s(i)=-1$ represents a share of deviational energy decrease relative to the reference state (the “deficient” phonon group in lower-temperature regions).
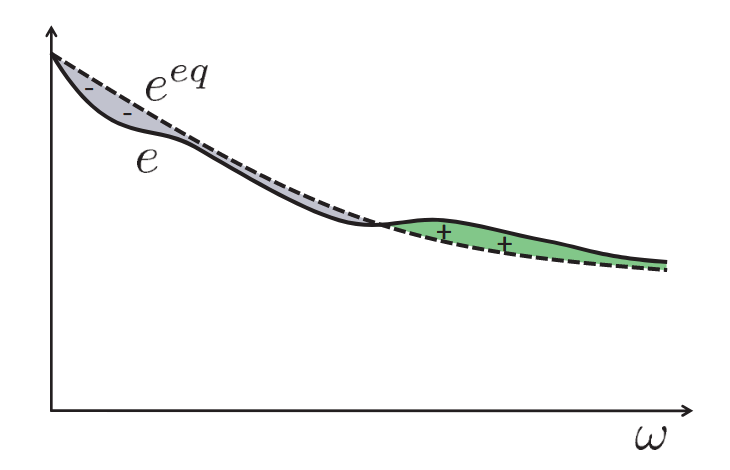
The deviational energy method focuses calculations on the non-equilibrium energy deviations by introducing a reference equilibrium temperature $T_\text{eq}$, rather than the full phonon distribution function. This reduces the simulation of large numbers of equilibrium phonons, significantly improving simulation efficiency, especially in cases of small temperature differences or near-equilibrium states.
In the deviational energy method, the number and sign (positive or negative) of simulated particles directly correspond to changes in deviational energy, reducing energy errors during particle addition or removal. Moreover, the computation inherently follows the principle of energy conservation.
2. Monte Carlo Simulation Algorithm
2.1 Particle-Based Simulation
Initialization:
At the initial temperature $T$, use BE statistics to calculate the number of phonons in volume $V$:
\[N=V\int_{\omega=0}^{\omega_\text{max}}\sum_p D(\omega,p) f_T^\text{eq}(\omega) d\omega\]The number of simulated particles (each representing a phonon bundle) is given by $N/N_\text{eff}$.
The value of $N_\text{eff}$ is determined by balancing computational cost and the number of particles needed to obtain statistically meaningful results.
Time Evolution:
After system initialization, the simulation is performed using a time-stepping algorithm with time step $\Delta t$. Each time step consists of three substeps:
1). Phonon Drift
During this period, simulated particle $i$ moves $\boldsymbol v_{g,i}\Delta t$.
2). Sampling
Record temperature ($T$) and pseudo-temperature ($T_\text{loc}$), which are computed by inverting the energy ($E$) and pseudo-energy ($\widetilde E$) relations:
\[E=N_\text{eff}\sum_i\hbar\omega_i=V\int_{\omega=0}^{\omega_\text{max}}\sum_p \frac{D(\omega,p) \hbar\omega}{\exp\left(\frac{\hbar\omega}{k_BT}\right)-1} d\omega\] \[\widetilde E=N_\text{eff}\sum_i\frac{\hbar\omega_i}{\tau(\omega_i,p_i,T)}=V\int_{\omega=0}^{\omega_\text{max}}\sum_p \frac{D(\omega,p) \hbar\omega}{\tau(\omega,p,T)}\frac{1}{\exp\left(\frac{\hbar\omega}{k_BT_\text{loc}}\right)-1} d\omega\]Temperature ($T$) represents the average temperature in thermal equilibrium, while pseudo-temperature ($T_\text{loc}$) is related to phonon scattering processes and used to analyze phonon behavior in non-equilibrium states.
3). Phonon Scatter
Perform scattering based on the scattering probability:
\[P_i = 1-\exp\left(-\frac{\Delta t}{\tau(\omega_i,p_i,T)}\right)\]Scattering is performed by sampling new frequencies, polarizations, and propagation directions. The post-scattering frequencies must be drawn from the distribution $D(\omega,p)f^\text{loc}/\tau(\omega,p,T)$.
During scattering, energy conservation must be ensured. However, since the frequency of scattered phonons is randomly sampled, particles need to be added or removed to approximate the target energy, enforcing energy conservation.
This method does not always guarantee energy conservation, causing the system’s energy to drift randomly and introducing deterministic errors.
2.2 Energy-Based Simulation
Using energy as the simulated particle, the algorithm is similar to the above but requires the following adjustments:
- During initialization, boundary emission, or scattering, the sampling of frequency distribution must include a correction factor $\hbar\omega$.
- Calculating energy within a grid is straightforward: simply count the number of particles. The energy of $N$ particles is given by $\varepsilon_\text{eff} N$.
- Since the energy within the grid is proportional to the number of particles, no addition or deletion process is needed: simply conserving the number of particles ensures strict energy conservation.
2.3 Deviational Energy-Based Simulation
Initialization:
First, select the equilibrium state at temperature $T_\text{eq}$ as the reference.
If the initial state $f^0$ matches the equilibrium distribution, no particles exist at the start of the simulation. The system’s deviational energy can be estimated based on the maximum temperature deviation:
\[\Delta E = \int_{\omega=0}^{\omega_\text{max}}\sum_p\hbar\omega D(\omega,p)\times \bigg|\frac{1}{\exp(\frac{\hbar\omega}{k_BT})-1}-\frac{1}{\exp(\frac{\hbar\omega}{k_BT_\text{eq}})-1}\bigg| d\omega\]The effective deviational energy $\varepsilon_\text{eff}^d$ can be roughly determined based on the desired number of simulated particles.
If the initial state $f^0$ differs from the equilibrium distribution, particles must be initialized. Their frequencies and polarizations are drawn from the distribution:
\[D(\omega,p)e^d(\omega) = \hbar\omega D(\omega,p)\bigg[f^0-\frac{1}{\exp(\frac{\hbar\omega}{k_BT_\text{eq}})-1}\bigg]\]Typically, $f^0$ is an equilibrium distribution at some temperature $T$, simplifying the above expression to:
\[D(\omega,p)e^d(\omega) = \hbar\omega D(\omega,p)\bigg[\frac{1}{\exp(\frac{\hbar\omega}{k_BT})-1}-\frac{1}{\exp(\frac{\hbar\omega}{k_BT_\text{eq}})-1}\bigg]\]If $T > T_\text{eq}$, this function is positive; if $T < T_\text{eq}$, it is negative. In the latter case, particles are assigned a negative sign.
Frequency sampling: By subdividing the frequency range into bins, define a discretized and normalized cumulative distribution according to the above equation. Uniformly draw a random number between 0 and 1, and use it to find the corresponding bin in the normalized cumulative distribution.
Time Evolution:
(1) Phonon Drift:
During the time step $\Delta t$, simulated particle $i$ moves $\boldsymbol v_{g,i}\Delta t$.
(2) Sampling:
(a) Let $C_j$ denote the set of particle indices in volume $V_j$ of cell $j$ at time $t$. Since each particle represents the same amount of energy, the deviational energy is:
\[\Delta E_j = \varepsilon_\text{eff}^d \sum_{i\in C_j} s(i) = \varepsilon_\text{eff}^d (N_j^+ - N_j^-)\]where $N_j^+$ and $N_j^-$ are the numbers of positive and negative particles in cell $j$, respectively.
(b) The corresponding temperature $T_j$ is calculated by numerically inverting the equation:
\[\frac{\Delta E_j}{V_j} = \int_0^{\omega_\text{max}}\sum_p D(\omega,p)\hbar\omega \bigg[\frac{1}{\exp(\frac{\hbar\omega}{k_BT_j})-1} - \frac{1}{\exp(\frac{\hbar\omega}{k_BT_\text{eq}})-1} \bigg] d\omega\](c) The pseudo-temperature $[T_\text{loc}]_j$ is calculated by numerically inverting:
\[\frac{\Delta \widetilde E_j}{V_j} = \int_0^{\omega_\text{max}}\sum_p \frac{D(\omega,p)\hbar\omega}{\tau(\omega,p,T_j)} \bigg[\frac{1}{\exp(\frac{\hbar\omega}{k_B[T_\text{loc}]_j})-1} - \frac{1}{\exp(\frac{\hbar\omega}{k_BT_\text{eq}})-1} \bigg] d\omega\] \[\Delta\widetilde E_j = \varepsilon^d_\text{eff} \sum_{i\in C_j}\frac{s(i)}{\tau(\omega_i,p_i,T_j)}\](3) Phonon Scatter:
Determine whether each phonon undergoes scattering based on the probability:
\[P(\omega_i, p_i, T_j) = 1 - \exp\left(-\frac{\Delta t}{\tau(\omega_i, p_i, T_j)}\right)\]Scattered phonons are replaced with new particles, whose attributes (frequency and polarization) are drawn from:
\[\frac{D(\omega, p)(e^\text{loc} - e^\text{eq}_{T_\text{eq}})}{\tau(\omega, p, T_j)} = \frac{D(\omega, p)\hbar\omega}{\tau(\omega, p, T_j)} \bigg[\frac{1}{\exp\left(\frac{\hbar\omega}{k_B [T_\text{loc}]_j}\right) - 1} - \frac{1}{\exp\left(\frac{\hbar\omega}{k_B T_\text{eq}}\right) - 1} \bigg]\]3. Setting Boundary Conditions
In phonon transport problems, various types of boundary conditions can arise: adiabatic boundaries, isothermal boundaries, and periodic boundaries.
3.1 Adiabatic Boundary
Adiabatic boundaries reflect all incident phonons. This reflection process can be divided into two main categories: diffuse reflection and specular reflection.
In both cases, it is assumed that the polarization and frequency of phonons remain unchanged upon reflection. The only parameter modified during this process is the direction of propagation.
(i) Specular reflection ensures energy conservation, $e^d(\boldsymbol x, \boldsymbol k) = e^d(\boldsymbol x, \boldsymbol k’)$, with the direction given by:
\[\boldsymbol k' = \boldsymbol k - 2(\boldsymbol k \cdot \boldsymbol n) \boldsymbol n\]where $\boldsymbol n$ is the normal vector of the boundary.
(ii) Diffuse reflection randomizes the reflection direction of phonons incident on the boundary, similar to how scattered phonons are treated.
Specular reflection occurs when the boundary is very smooth (relative to the phonon wavelength), meaning the surface roughness of the boundary is much smaller than the phonon wavelength. Specular reflection does not randomize the phonon distribution, allowing phonons to maintain directional transport.
Diffuse reflection occurs when the boundary roughness is comparable to or larger than the phonon wavelength. Diffuse reflection leads to an isotropic phonon distribution, reducing the efficiency of phonon heat transfer. In nanostructures, diffuse reflection enhances phonon-boundary scattering effects, significantly reducing the material’s effective thermal conductivity.
3.2 Isothermal Boundary
Under isothermal boundary conditions at temperature $T_b$, phonons incident on the boundary are completely absorbed. The boundary then re-emits phonons according to its own temperature $T_b$, following the equilibrium distribution.
The emitted heat flux per unit angular frequency can be expressed as:
\[q_{\omega,b}'' = \frac{1}{4} \sum_p \frac{D(\omega,p)v_g(\omega,p)\hbar\omega}{\exp\left(\frac{\hbar\omega}{k_B T_b}\right) - 1}\]In deviational energy-based simulations, the difference in heat flux between the isothermal boundary and the reference equilibrium temperature $T_\text{eq}$ must be considered. The corrected expression is given by:
\[q_{\omega,b}'' = \frac{1}{4} \sum_p D(\omega,p)v_g(\omega,p)\hbar\omega \cdot \bigg[\frac{1}{\exp\left(\frac{\hbar\omega}{k_B T_b}\right) - 1} - \frac{1}{\exp\left(\frac{\hbar\omega}{k_B T_\text{eq}}\right) - 1} \bigg]\]This formula provides the frequency distribution of emitted particles under isothermal boundary conditions. Specifically, it reflects the non-equilibrium phonon transport characteristics of the boundary at temperature $T_b$, i.e., how the boundary absorbs and re-emits phonons based on the temperature difference.
3.3 Periodic Boundary
Periodic boundary conditions allow the simulation of a complete structure by considering only a single unit cell (period).
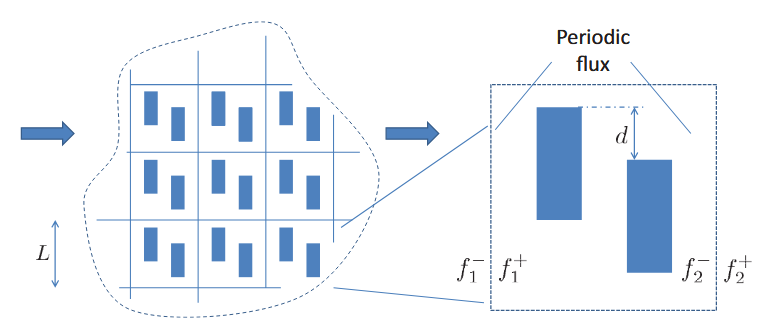
At the boundary, deviations in phonon distribution from local equilibrium are periodic and can be described by the following relations:
\[f_1^+ - f_{T_1}^\text{eq} = f_2^+ - f_{T_2}^\text{eq}\] \[f_1^- - f_{T_1}^\text{eq} = f_2^- - f_{T_2}^\text{eq}\]Here, $f_{T_1}^\text{eq}$ and $f_{T_2}^\text{eq}$ denote the equilibrium distributions at temperatures $T_1$ and $T_2$, respectively. The superscript $+$ represents particles moving to the right, while $-$ represents particles moving to the left. This formula reflects both the periodicity of heat flux and the temperature gradient.
For deviational energy distribution, this relationship becomes:
\[\hbar\omega(f_1^+ - f_{T_\text{eq}}^\text{eq} - f_{T_1}^\text{eq}) = \hbar\omega(f_2^+ - f_{T_\text{eq}}^\text{eq} - f_{T_2}^\text{eq})\] \[\hbar\omega(f_1^- - f_{T_\text{eq}}^\text{eq} - f_{T_1}^\text{eq}) = \hbar\omega(f_2^- - f_{T_\text{eq}}^\text{eq} - f_{T_2}^\text{eq})\]Expressed in terms of deviational energy:
\[e_1^{d,+} - e_{T_1}^\text{eq} = e_2^{d,+} - e_{T_2}^\text{eq}\] \[e_1^{d,-} - e_{T_1}^\text{eq} = e_2^{d,-} - e_{T_2}^\text{eq}\]Periodic boundary conditions can be enforced as follows:
(i) Remove particles crossing the periodic boundary from one side of the system and reinsert them on the other side, keeping their properties unchanged.
(ii) Generate new particles at the boundary: these particles have directions randomized over a hemisphere. At the hot boundary, they are emitted to the right with a positive sign, while corresponding negative particles are emitted from the cold boundary. Particle generation follows the distribution:
\[(e_{T_1}^\text{eq}-e_{T_2}^\text{eq})\frac{D(\omega,p)}{4\pi} v_g(\omega,p)\]References:
[1] S. Mazumder, A. Majumdar, Monte Carlo Study of Phonon Transport in Solid Thin Films Including Dispersion and Polarization, Journal of Heat Transfer 123 (2001) 749–759.
[2] Q. Hao, G. Chen, M.-S. Jeng, Frequency-dependent Monte Carlo simulations of phonon transport in two-dimensional porous silicon with aligned pores, Journal of Applied Physics 106 (2009) 114321.
[3] J.-P.M. Péraud, N.G. Hadjiconstantinou, Efficient simulation of multidimensional phonon transport using energy-based variance-reduced Monte Carlo formulations, Phys. Rev. B 84 (2011) 205331.