Numerical Methods for Density of States (DOS) Calculation
One of the most critical quantities in lattice dynamics studies is the density of states (DOS), defined as the number of normal modes within the frequency range $\omega$ and $\omega + d\omega$.
Expression for DOS:
\[\text{DOS}(\omega) = \frac{V}{8\pi^3} \sum_s \int \frac{dS_\omega}{|\Delta_{\boldsymbol k}\omega_s|}\]where $S_\omega$ is the isofrequency surface.
Root Sampling Method
This is the simplest method (also known as the histogram statistical method):
\[\text{DOS}(\omega) = \frac{V}{8\pi^3} \sum_{\boldsymbol qs} \delta(\omega - \omega(\boldsymbol qs))\]Using this method, we can count the number of modes within $\Delta\omega$ to obtain the density of states. However, this method requires a large number of $\boldsymbol k$ points in the Brillouin zone (the grid needs to be sufficiently dense) to achieve accurate results.
Linear Extrapolation
The GR method divides the irreducible part of the first Brillouin zone into a uniform simple cubic grid with points $\boldsymbol k_c$ spaced by $2b$. Each point $\boldsymbol k_c$ is at the center of a small cube. From the small cube containing each $\boldsymbol k_c$, “all” frequencies are extracted, and the contributions from all cubes are summed to obtain the complete frequency distribution.
The eigenfrequency at $\boldsymbol k_c$ is $\omega(\boldsymbol k_c)$. Assuming linear extrapolation is valid within each small cube, the isofrequency surface can be represented as parallel planes perpendicular to $\nabla\omega(\boldsymbol k_c)$. The volume element $dV$ between two such parallel planes corresponds to the number of frequencies within $\omega$ and $\omega + d\omega$. When $dV$ approaches zero, it can be approximated as
\[dV = Sd k_\perp\]where $S$ is the cross-sectional area of the plane within the cube, and $d k_\perp$ is the thickness of the volume element.
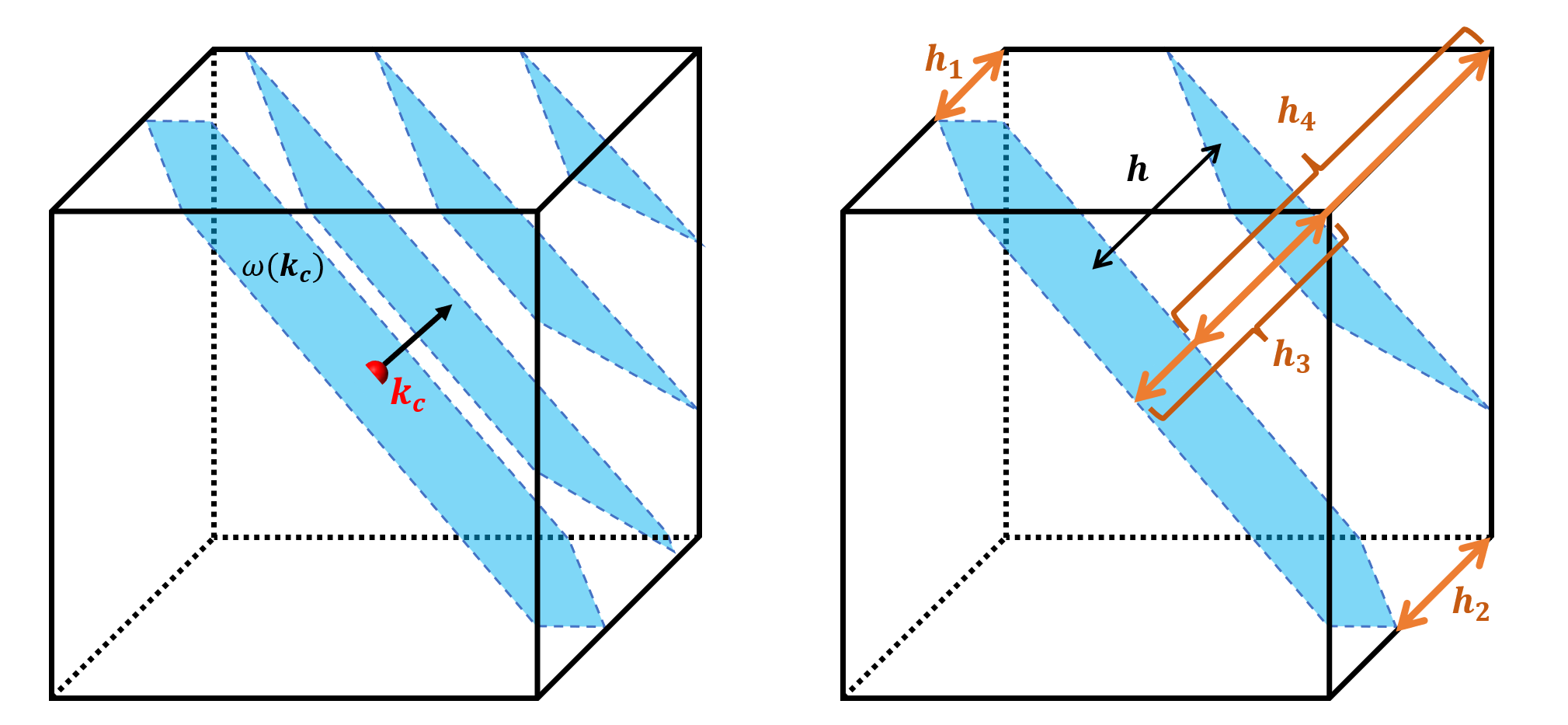
Next, consider the cross-sectional area of this set of isofrequency planes within the cube. First, assume the three direction cosines of the normal to the isofrequency plane are $l_1$, $l_2$, and $l_3$, sorted in descending order.
For any cross-section at a distance $h$ from $\boldsymbol k_c$, the cross-sectional area is denoted as $S(h)$. It must satisfy $S(h) = S(-h)$, so we only need to consider half of the cube ($h > 0$).
List in ascending order the distances of the four corners in this half to the plane passing through the cube center:
\(h_1 = b|l_1 - l_2 - l_3|\) \(h_2 = b(l_1 - l_2 + l_3)\) \(h_3 = b(l_1 + l_2 - l_3)\) \(h_4 = b(l_1 + l_2 + l_3)\)
In the first range $(0 \leq h \leq h_1)$, there are two possibilities depending on the sign of $(l_1 - l_2 - l_3)$. If the sign is positive, the cross-section is a parallelogram with an area of
\[S(h) = \frac{4b^2}{l_1}\]If it is negative, the cross-section is a hexagon with an area of
\[S(h) = \frac{2b^2(l_1 l_2 + l_2 l_3 + l_3 l_1) - (h^2 + b^2)}{l_1 l_2 l_3}\]In the second range $(h_1 \leq h \leq h_2)$, the shape is a pentagon, and its area is
\[S(h) = \frac{2b^2(l_1 l_2 + 3l_2 l_3 + l_3 l_1) - bh(-l_1 + l_2 + l_3) - \frac{1}{2}(h^2 + b^2)}{l_1 l_2 l_3}\]In the third range $(h_2 \leq h \leq h_3)$, the shape is a quadrilateral, and its area is
\[S(h) = \frac{2b^2 l_3(l_1 + l_2) - bhl_3}{l_1 l_2 l_3}\]In the fourth range $(h_3 \leq h \leq h_4)$, the shape is a quadrilateral, and its area is
\[S(h) = \frac{[b(l_1 + l_2 + l_3) - h]^2}{2l_1 l_2 l_3}\]These expressions and their derivatives are continuous at their respective boundaries, and $S(h)$ integrated over the entire range yields the volume of the cube.
Linear extrapolation over the entire cube provides the frequency variation:
\[\Omega = \omega(\boldsymbol k_c) \pm h\nabla\omega(\boldsymbol k_c)\]where $0 \leq h \leq h_4$.
To construct $\text{DOS}(\omega)$, we define a function $g_s(\boldsymbol k_c, \omega)$, which is the frequency distribution obtained by linearly extrapolating the entire cube centered at $\boldsymbol k_c$:
\[g_s(\boldsymbol k_c, \omega) = CW(\boldsymbol k_c) S_s(h)dh = CW(\boldsymbol k_c) S_s(w) \frac{d\omega}{|\nabla\omega(\boldsymbol k_c)|}\]where $\omega(\boldsymbol k_c) - h_4\nabla\omega(\boldsymbol k_c) \leq \omega \leq \omega(\boldsymbol k_c) + h_4\nabla\omega(\boldsymbol k_c)$.
Here, $C$ is a normalization constant, and $W(\boldsymbol k_c)$ is the symmetry-related weight factor for point $\boldsymbol k_c$.
Finally, the complete density of states:
\[\text{DOS}(\omega) = \sum_{\boldsymbol k_c, s} g_s(\boldsymbol k_c, \omega)\]The GR method has two practical challenges: (i) It requires the gradient $\nabla\omega(\boldsymbol k_c)$ to be calculated first. (ii) Since the cubes do not typically conform exactly to the Brillouin zone, it is necessary to determine the statistical weights of the cubes in the irreducible part of the zone.
Generalization of Linear Extrapolation
The core idea of the GGR method is to use an affine transformation to convert the parallelepiped-shaped Brillouin zone into a cube, enabling the original GR method to be applied to any lattice.
The BZ is a parallelepiped defined by three reciprocal vectors $\boldsymbol b_i (i = 1, 2, 3)$. The $\boldsymbol k$ points are uniformly distributed along the three basis vectors $\boldsymbol b_i$.
An affine transformation changes the $\boldsymbol k$ basis of the parallelepiped BZ to the $\boldsymbol t = (t_1, t_2, t_3)$ cubic basis:
\[\boldsymbol k = \boldsymbol b_1 t_1 + \boldsymbol b_2 t_2 + \boldsymbol b_3 t_3\]where $t_1, t_2, t_3 \in [0, 1]$.
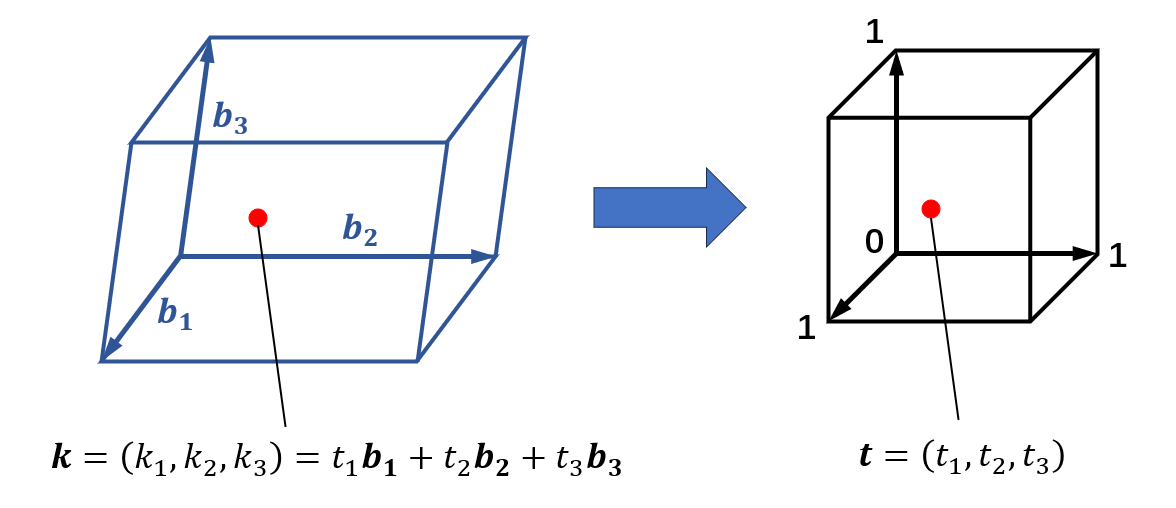
The volume elements of the two bases satisfy $dV_k = \det(B)dV_t = \Omega dV_t$, where $\Omega$ is the volume of the BZ.
We transform $\text{DOS}(\omega)$ (the integral over the isofrequency surface $S_\omega$) from the $\boldsymbol k$ basis to the $\boldsymbol t$ cubic basis:
\[\text{DOS}(\omega) = \frac{1}{\Omega} \sum_s \int_{S_\omega} \frac{dS_k}{|\Delta_{\boldsymbol k}\omega_s|} = \sum_s \int_{S_\omega} \frac{dS_t}{|\Delta_{\boldsymbol t}\omega_s|}\]Linear Interpolation
The irreducible part is divided into multiple tetrahedra of equal volume. The phonon frequency at each vertex of the tetrahedron is known, and the phonon frequency $\nabla\omega(\boldsymbol k)$ at any position inside the tetrahedron can be obtained by linear interpolation:
\[\omega(\boldsymbol k) = a_1\omega(\boldsymbol k_1) + a_2\omega(\boldsymbol k_2) + a_3\omega(\boldsymbol k_3) + a_4\omega(\boldsymbol k_4)\]where $a_i$ are the weighting coefficients at the vertices of the tetrahedron, satisfying $a_1 + a_2 + a_3 + a_4 = 1$. These weights depend on the position of point $\boldsymbol k$ inside the tetrahedron.
The tetrahedron method only requires the distribution of $\omega(\boldsymbol k_i)$ on a coarse grid and does not require frequency gradients (group velocity).
However, at band crossings or degenerate points, linear interpolation introduces errors.
Enjoy Reading This Article?
Here are some more articles you might like to read next: