Phonon Dispersion Calculation of Silicon Using QE

Phonon dispersion in Quantum Espresso is calculated using the ph.x program, based on Density Functional Perturbation Theory (DFPT). This article demonstrates the calculation process using monocrystalline silicon (Si) as an example.

Step 1 pw.x

Perform SCF calculation using pw.x.

• SCF Input File (pw.scf.Si.in)

&control
  calculation = 'scf'
  restart_mode = 'from_scratch'
  pseudo_dir = './pseudos/'
  outdir = './out/'
  prefix = 'Si'
/
&system
  ibrav = 2
  celldm(1) = 10.20
  nat = 2
  ntyp = 1
  ecutwfc = 16
/
&electrons
  mixing_mode = 'plain'
  mixing_beta = 0.7
  conv_thr = 1.0e-8
/
ATOMIC_SPECIES
  Si 28.0855 Si.vbc.UPF
ATOMIC_POSITIONS
  Si 0.00 0.00 0.00
  Si 0.25 0.25 0.25
K_POINTS {automatic}
  8 8 8 0 0 0

• Execute SCF Calculation

mpirun -np 4 pw.x -i pw.scf.Si.in > pw.scf.Si.out

Step 2 ph.x

Compute dynamical matrices on a uniform q-point grid using ph.x.

• Input File (ph.Si.in)

&INPUTPH
  tr2_ph = 1d-14
  amass(1) = 28.0855
  ldisp = .true.
  nq1 = 4
  nq2 = 4
  nq3 = 4
  outdir = './out/'
  prefix = 'Si'
  fildyn = 'Si.dyn'
/

• Execute Calculation

mpirun -np 4 ph.x -i ph.Si.in > ph.Si.out

• Output Files

Si.dyn0 contains the coordinates of the q-point grid.
Si.dyn1-N contains force constants ( C(q_n) ), where ( n = 1,…N ), with ( N ) being the number of irreducible q-points in the Brillouin zone.

Step 3 q2r.x

Use q2r.x to perform an inverse Fourier transform of the force constants in q-space to obtain real-space force constants.

• Input File (q2r.Si.in)

&INPUT
  fildyn = 'Si.dyn'
  zasr = 'simple' 
  flfrc = 'Si444.fc'
/

• Execute Calculation

mpirun -np 4 q2r.x -i q2r.Si.in > q2r.Si.out

• Output File

Si444.fc contains real-space force constants for a 4×4×4 supercell.

Step 4 matdyn.x

Use matdyn.x to perform a Fourier transform on real-space components to obtain the dynamical matrix and eigenvalues (frequencies) at arbitrary q-points.

• Input File (matdyn.Si.in)

&INPUT
  asr = 'simple'  
  flfrc = 'Si444.fc'
  flfrq = 'Si.freq'  
  flvec = 'Si.modes' 
  q_in_band_form = .true.
/
6
0.000 0.000 0.000   50
0.500 0.000 0.500   50
0.625 0.250 0.625   1
0.375 0.375 0.750   50
0.000 0.000 0.000   50
0.500 0.500 0.500    1

• Execute Calculation

mpirun -np 4 matdyn.x -i matdyn.Si.in > matdyn.Si.out

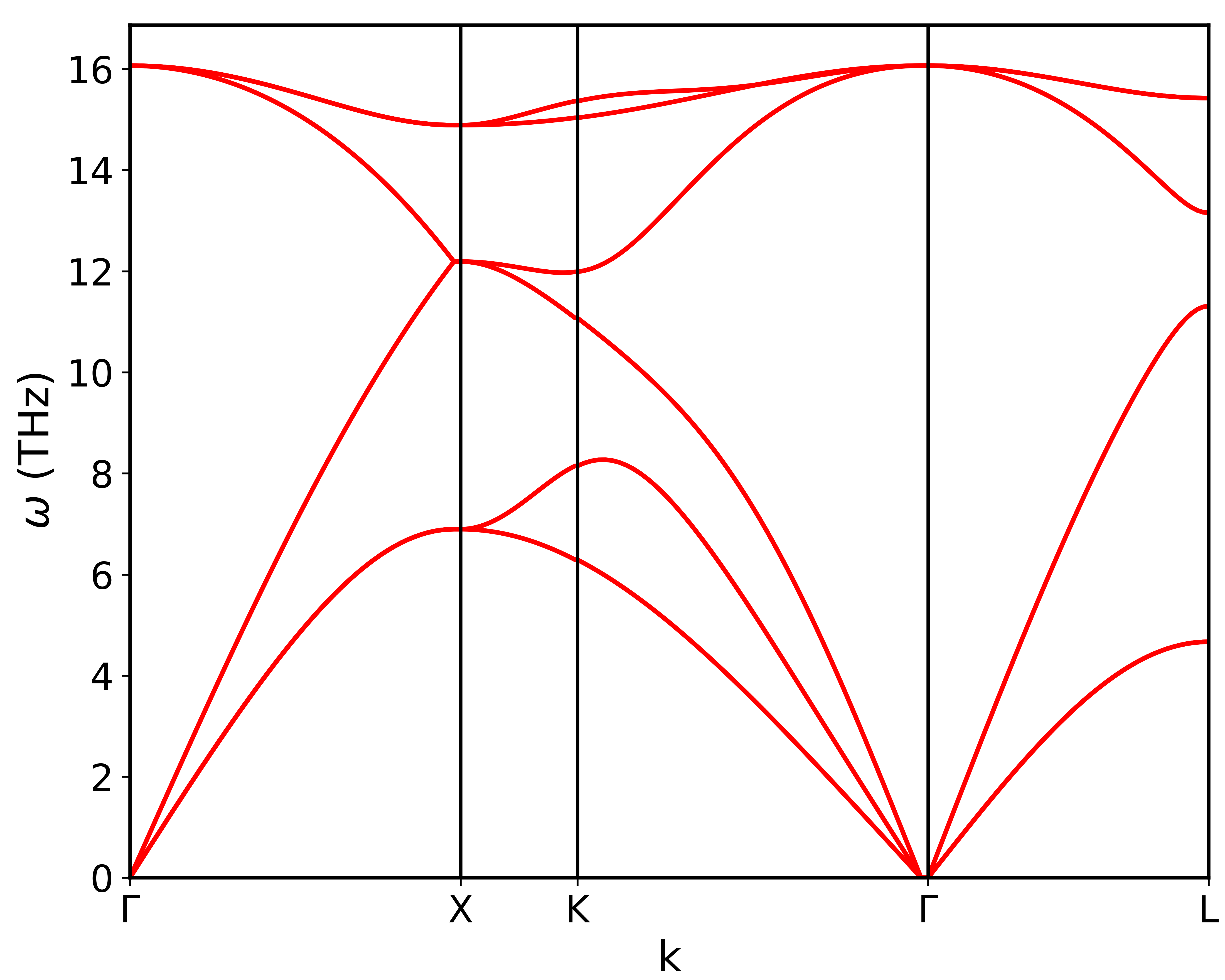
Then, use the resulting Si.freq.gp file to generate plots.